Symmetric Matrices Eigenvalues Proof

Let u 1 u n be the linearly independent eigenvectors which correspond to the positive eigenvalues λ 1 λ n of the real symmetric matrix A. The entries of a symmetric matrix are symmetric with respect to the main diagonal.

Pin On Math Videos

Ahas real eigenvalues 1.

Symmetric matrices eigenvalues proof. Alternatively we can say the following. In fact the rst bullet implies the second think about why and moreover these bullets have the implication that A Q Q 1. Now A QΛQT because QT Q1.

Note that it is an orthogonal matrix so deserves to be called Q. A Hermitian symmetric matrix with all positive eigenvalues must be positive definite. Therefore HPD SPD matrices MUST BE INVERTIBLE.

RnRn is a symmetric matrix then A has eigenvectors v 1v n such that fv 1v ngis an or-thonormal basis for Rn. If s a bi is a complex number let s a bi. If is an eigenvalue of Q for some x 0 we have the following chains of equations.

A is real because Q and Λ are. Symmetric matrices have real eigenvalues The Spectral Theorem states that if Ais an n nsymmetric matrix with real entries then it has northogonal eigenvectors. Proposition 3 If Q is a real symmetric matrix all of its eigenvalues are real numbers.

The eigenvalues of A are real to see this suppose Av λv v 6 0 v Cn then vTAv vTAv λvTv λ Xn i1 vi2 but also vTAv Av T v λv T v λ Xn i1 vi2. Also let z c 1 u 1 c n u n be a random n 1. It remains to show that if aib is a complex eigenvalue for the real symmetric matrix A then b 0 so the eigenvalue is in fact a real number.

The trace of a symmetric matrix A2R n is equal to the sum of its eigenvalues. VH i v j 0. Let Q be the matrix of eigenvectors.

Then the eigenvalues of Aare real and the eigenvectors are orthogonal in the Hermitian sense. We will show b 0 by considering v tiw Aviw. Symmetric matrices and positive definiteness Symmetric matrices are good their eigenvalues are real and each has a com plete set of orthonormal eigenvectors.

The proof is by induction on the size of the matrix. Qx x Qx x Q x x xTQx xTQ x xT x xTx. Theorem 1 The spectral theorem for symmetric matrices.

Do your results agree with Theorem 571. A useful consequence of HPD SPD matrices is that their eigenvalues which wealreadyknowarerealdue to the Hermitianpropertymust be NON-NEGATIVE. Eigenvalues of symmetric matrices suppose A Rnn is symmetric ie A AT fact.

Under the conditions of Theorem 1 in case p0 we haue 7 E VJAI 2o i onltlogn with prob. Hence the eigenvalues of a skew symmetric matrix are real. The eigenvalues of A are real numbers.

Symmetric matrices are good their eigenvalues are real and each has a com plete set of orthonormal eigenvectors. Its a Markov matrix its eigenvalues and eigenvectors are likely. Let Abe a Hermitian matrix.

And just check that AT QTTΛTQT. Grinfelds Tensor Calculus textbookhttpslemmaprep - C. Symmetric matrices A symmetric matrix is one for which A AT.

If a matrix has some special property eg. This proves the remarkable fact that the eigenvectors of a symmetric matrix are mutually orthogonal. We can decompose any symmetric matrix with the symmetric eigenvalue decomposition SED where the matrix of is orthogonal that is and contains the eigenvectors of while the diagonal matrix contains the eigenvalues of.

HttpsbitlyPavelPatreonhttpslemmaLA - Linear Algebra on LemmahttpbitlyITCYTNew - Dr. THE EIGENVALUES OF RANDOM SYMMETRIC MATRICES 235 Theorem 2. Suppose v iw 2 Cn is a complex eigenvector with eigenvalue aib here vw 2 Rn.

Positive definite matrices are even bet ter. The trace of a square matrix is the sum of its diagonal entries. Tending to I Thus we see that though the semi-circle law allows on eigenvalues to be larger than 2oln 6nfacttheycould be arbitrarily large there is at most one.

Where Q 0 j j v 1 v n j j 1 Ais an orthogonal matrix and 0 1. And since it must be that and so and are orthogonal. 1012 Trace Determinant and Rank De nition 102.

Eigenvalue decomposition for symmetric matrices. Two special functions of eigenvalues are the trace and determinant described in the next subsection. Show that the following symmetric matrices are positive definite and calculate their eigenvalues.

The rst step of the proof is to show that all the roots of the characteristic polynomial of Aie. Then st s t s is real if and only if s s and s s a2 b2. Formally A is symmetric A A T.

Note that applying the complex conjugation to the identity Aviw aibviw yields Av iw a ibv iw. I want to talk about the di usion of heat around a circular loop of wire. A matrix has all real eigenvalues and n orthonormal real eigenvectors if and only if it is real symmetric.

Thus distinct eigenspaces of a skew symmetric matrix are orthogonal. On the one hand this is. If a matrix is symmetric the eigenvalues are REAL not COMPLEX numbers and the eigenvectors could be made perpendicular orthogonal to each other.

In linear algebra a symmetric matrix is a square matrix that is equal to its transpose. This is a sketch of a proof when the symmetric matrix A is real. So if a i j displaystyle a_ij denotes the entry in the i displaystyle i th row and j displaystyle j th column then A is symmetric f.

Returning to the case with now known to be real and so Equation becomes. Displaystyle Atext is symmetriciff AAtextsf T Because equal matrices have equal dimensions only square matrices can be symmetric.

Understanding A Proof Eigenvalues Of A Real Symmetric Matrix Are Real Mathematics Stack Exchange

Proof Of Formula For Determining Eigenvalues Video Khan Academy

Pin On Proof Videos

Pin On Math Videos

Pin On Linear Algebra Videos

Real Symmetric Matrices Have Only Real Eigenvalues Is This An Incorrect Proof Mathematics Stack Exchange

Karl Stratos Research Eigentutorial

Karl Stratos Research Eigentutorial

A State The Spectral Theorem For Symmetric Chegg Com

How To Prove A Matrix Is Symmetric Youtube

Karl Stratos Research Eigentutorial

Prove The Ell 2 Norm Of A Linear Transformation A Mathbb R N To Mathbb R N Is The Maximum Eigenvalue Mathematics Stack Exchange

Proof For Why Symmetric Matrices Are Only Orthogonally Diagonalizable Mathematics Stack Exchange

Pin On Linear Algebra Videos

Proof For Why Symmetric Matrices Are Only Orthogonally Diagonalizable Mathematics Stack Exchange

Pin On Proof Videos

Pin On Linear Algebra Videos

6 4 10 Introduction To Linear Algebra Strang Here Quick Proof That The Eigenvalues Of All Real Matrices Are Exercises On Symmetric Matrices And Positive Definiteness Problem 25 1

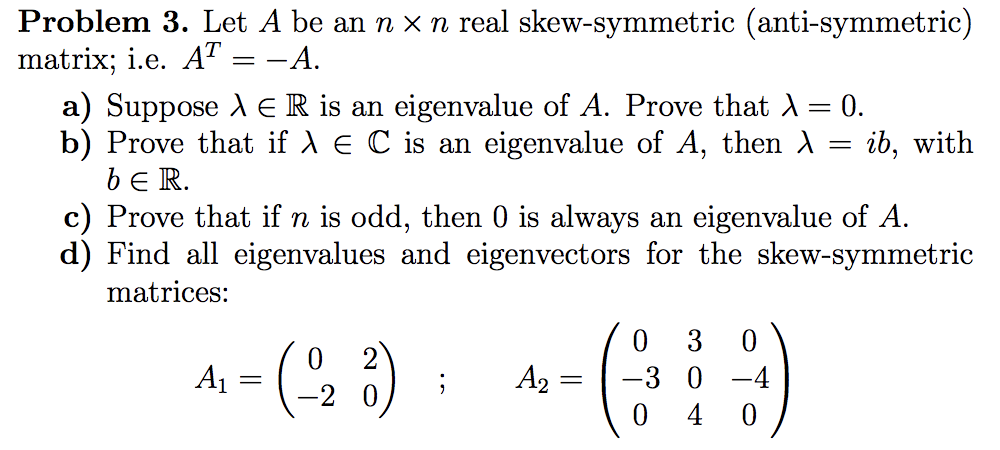
Problem 3 Let A Be An N X N Real Skew Symmetric Chegg Com