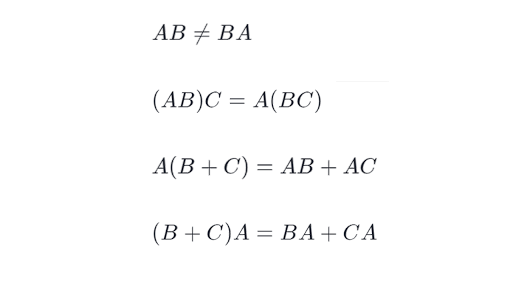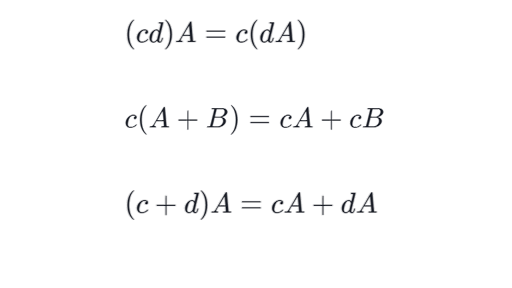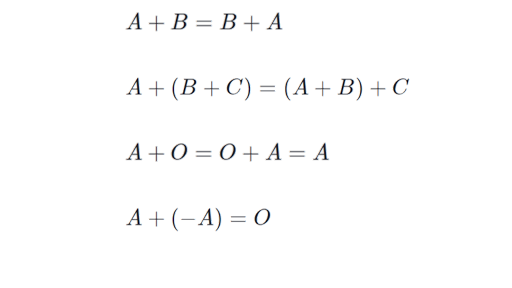Matrix Inverse Properties Addition
Existence of Additive Inverse. Iv Existence of additive inverse.

Theorem 2 1 Properties Of Matrix Addition And Scalar Chegg Com
Let A a ij mn be any matrix then we have another matrix as A a ij mn such that A A A A O.

Matrix inverse properties addition. Is the Inverse Property of Matrix Addition similar to the Inverse Property of Addition. 11 where I is the identity matrix. To find additive inverse of a given matrix A we need to find a matrix which when added to the given matrix produces null matrix or zero matrix.
If matrix Q has to be subtracted from matrix P then we will take the inverse of matrix Q and add it to matrix P. 3 rows For example if then. It is noted that in order to find the matrix inverse the square matrix should be non-singular whose determinant value does.
The additive inverse ofAis A. Null or zero matrix is the additive identity for matrix addition. So A is the additive inverse of A or negative of A.
MN ad bc 0 0 ad bc. Ad bcI Then M 1 1 ad bc d b c a so long as ad bc 6 0. Only square matrices can have an inverse.
A A AA 0 where0is the zero matrix here. But we can multiply a matrix by its inverse which is kind of. A O O A A.
If A is a non-singular square matrix there is an existence of n x n matrix A-1 which is called the inverse of a matrix A such that it satisfies the property. Let P and. If a matrix A is invertible then it commutes with its inverse.
First if you are multiplying a matrix by its inverse the order does not matter. This equation cannot be used to calculate A B 1 but it is useful for perturbation analysis where B is a perturbation of A. Inverse of a 2 2 Matrix Let M and N be the matrices.
We prove part 1 and leave the other parts as exercises. In simpler words we can say that O is the additive identity for matrix addition. B A A B O.
To get additive inverse of given matrix we just need to multiply each element of matrix with -1. First let us define what it means for a matrix to be invertible and what a matrix inverse is. If A is a matrix of size m n and B is a matrix of.
Not every square matrix has an inverse. The identity matrix for the 2 x 2 matrix is given by. Multiplying these matrices gives.
A matrix M 1 such that M 1M I M 1M. AA-1 A-1A I where I is the Identity matrix. In fact this tutorial uses the Inverse Property of Addition.
Properties of matrix operations The operations are as follows. Where O is the null matrix of order m x n. One application of this is that to check that a.
In this case we call the matrix B the inverse of the matrix A which we denote as A 1. Since matrix additionsubtraction amounts to addingsubtracting cor-responding entries these properties will follow from the same properties of realnumbers. When we multiply each element of matrix with.
In this video you will learn about Properties of Matrix for Addition - Commutative Associative and Additive Inverse - Matrices - Maths - Class 12XII - ISCE. N d b c a. The Existence of Additive Inverse.
In other words AA1 A1A. A square matrix A is said to be invertible if there exists an matrix B such that ABBAI. We learned about matrix multiplication so what about matrix division.
There are a couple of properties to note about the inverse of a matrix. So A can be known as the additive inverse. For a matrix A B is called the additive inverse of A if.
Three Properties of the Inverse 1If A is a square matrix and B is the inverse of A then A is the inverse of B since AB I BA. It is shown in On Deriving the Inverse of a Sum of Matrices that A B 1 A 1 A 1 B A B 1. Each matrix has an additive inverse.
Let matrix A a ij mn be any matrix then we have another matrix as A a ij mn such that A A is equal to A A O. Mathematically In other words it can be said that matrix subtraction is an addition of the inverse of a matrix to the given matrix ie. Matrix multiplication is not commutative.
You can download Matrices Cheat Sheet by clicking on the download button below. There is no such thing. M a b c d.
If A is a matrix of order m x n then. Properties of Matrices Inverse. If A and B are matrices of the same size m n then A B their sum is a matrix of size m n.
This is highly unusual for matrix. A - A - A A O-A is the additive inverse of A. That is in general AB BA 3.
If A is a matrix of size m n and c is a scalar then cA is a matrix of size m n. If we add to we get a zero matrix which illustrates the additive. There are several other variations of the above form see equations 22- 26 in this paper.
Properties Of Matrix Multiplication Article Khan Academy
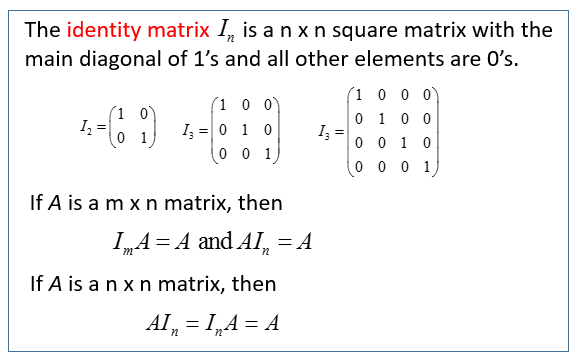
Zero Identity And Inverse Matrices Solutions Examples Videos Worksheets Games Activities

Chap 2 Matrices 2 1 Operations With Matrices Ppt Video Online Download

Chap 2 Matrices 2 1 Operations With Matrices Ppt Video Online Download

Inverse Matrices And Their Properties Youtube

Ppt Chapter 2 Matrices Powerpoint Presentation Free Download Id 1568385

Chap 2 Matrices 2 1 Operations With Matrices Ppt Video Online Download
Properties Of Matrix Scalar Multiplication Article Khan Academy

Addition Of Matrices Methods Concepts Properties Videos Examples

Theorem 2 1 Properties Of Matrix Addition And Scalar Chegg Com

Linear Algebra Learning The First Chapter And The Matrix Equations 1 4 Matrix Algebra Programmer Sought

2 1 Operations With Matrices 2 2 Properties Of Matrix Operations Ppt Video Online Download
Properties Of Matrix Addition Article Khan Academy

2 1 Operations With Matrices 2 2 Properties Of Matrix Operations Ppt Video Online Download

Ppt Chapter 2 Matrices Powerpoint Presentation Free Download Id 1568385

Matrix Inverse Properties Youtube

2 1 Operations With Matrices 2 2 Properties Of Matrix Operations Ppt Video Online Download