Matrix Chain Multiplication Minimum Cost Calculator
D -- array of dimensions of arrays 1. That is we calculate in the order.
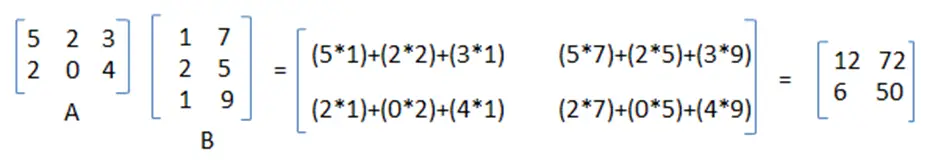
Matrix Chain Multiplication In C And C The Crazy Programmer
The Chain Matrix Multiplication Problem Given dimensions corresponding to matr 5 5 5 ix sequence 5 5 5.

Matrix chain multiplication minimum cost calculator. A i A i1A k. Should fill the table in increasing order of the length of the matrix-chain. A n so as to minimize the total cost assuming that the cost of multiplying an p i 1 p i matrix by a p i p i 1 matrix using the naive algorithm is p i 1 p i p i 1.
Step-1 For all values of ij set 0. Find the minimum cost of multiplying out of each subsequence. M ij equals the minimum cost for computing the sub-products A ik and A k1j plus the cost of multiplying these two matrices together.
After calculation you can multiply the result by another matrix right there. COSC 581 Algorithms. Do this for each possible position at which the sequence of matrices can be split and take the minimum over all of them.
P 40 20 30 10 30 Output. Matrix multiplication is not commutative but it is associative. M 3 5 M 3 M 4 M 5 There are two cases by which we can solve this multiplication.
Take the sequence of matrices and separate it into two subsequences. Here you can perform matrix multiplication with complex numbers online for free. To find the best possible way to calculate the product we could simply parenthesis the expression in every possible fashion and count each time how many scalar multiplication are required.
1 What is minimum number of scalar multiplications required to compute the product A 1 A 2 A n. The problem is not actually to perform the multiplications but merely to decide in which order to perform the multiplications. M 3 x M 4 M 5 M 3 M 4 xM 5.
Bottom Up Algorithm to Calculate Minimum Number of Multiplications. First a brief introduction is given about what is matrix chain multiplication problem and how to calculate the cost of multiplying. The optimum cost can be described by the following.
The paper is organized in following sections. Now resultant AB get dimensions 1 x 3 this multiplied with C need 132 6 multiplications. As Comparing both output 1320 is minimum in both cases so we insert 1320 in table and M 2 M 3 x M 4 this combination is chosen for the output making.
Ci j for j i is the minimum cost of multiplying for all breakpoints k viz. Matrix Chain Multiplication Firstly we define the formula used to find the value of each cell. To calculate AB we need 123 6 multiplications.
Note that this algorithm does not perform the multiplications it just figures out the best order in which to perform the multiplication operations. Then the cost of the solution to our problem is c1 n. Add these costs together and add in the cost of multiplying the two result matrices.
Approach has been described to calculate the minimum cost required to compute the chain multiplication using greedy approach. Matrix Chain Order Problem Given matrices A 1 A 2 A n where A i is a d i-1 x d i matrix. We need to write a function MatrixChainOrder that should return the minimum number of multiplications needed to multiply the chain.
Algorithm for Location of Minimum Value. The proposed method is named as Greedy MCM. Let the input 4 matrices be A B C and D.
Matrix Chain Multiplication Problem can be stated as find the optimal parenthesization of a chain of matrices to be multiplied such that the number of. However matrices can be not only two-dimensional but also one-dimensional vectors so that you can multiply vectors vector by matrix and vice versa. The idea of this algorithm is to find the minimum number of multiplication operations needed to multiply a chain of matrices.
Dynamic Programming Set 8 Matrix Chain Multiplication Given a sequence of matrices find the most efficient way to multiply these matrices together. We are given the sequence 4 10 3 12 20 and 7. Add these costs together and add in the cost of multiplying the two matrices.
Take the sequence of matrices and separate it into two subsequences. Find the minimum cost of multiplying out each subsequence. 26000 There are 4 matrices of dimensions 40x20 20x30 30x10 and 10x30.
N -- Number of arrays. If we follow second way ie. There is no cost associated with a single matrix subproblem so ci i 0.
2 What order of matrix multiplications achieves this minimum. Let ci j be the best cost or minimum value for multiplying in the subproblem A i A i1A j. Consider a chain of matrices.
Total 66 12 multiplications needed. The matrices have size 4 x 10 10 x 3 3 x 12 12 x 20 20 x 7. M 11 tells us about the operation of multiplying matrix A with itself which will be 0.
Matrix Chain Multiplication. Do this for each possible position at which the sequence of matrices can be split and take the minimum over all of them. Matrix chain multiplication calculator i the lower triangle stores the path p that was used for the lowest cost.
Let each matrix A i be p i-1 by p i. Because matrix multiplication is associative there can be more than one way of multiplying the chain of matrices and each way could incur a different number of multiplication operations. Example of Matrix Chain Multiplication Example.
The total cost is 48.

Matrix Chain Multiplication In C Codespeedy

Optimum Order For Matrix Chain Multiplications Prismoskills

Massive Algorithms Matrix Chain Multiplication
Matrix Chain Multiplication Using Dynamic Programming Algotree

Matrix Chain Multiplication Using Dynamic Programming Pencil Programmer

Matrix Chain Multiplication Dp 8 Tutorialspoint Dev

Matrix Chain Multiplication Using Dynamic Programming By Chetan More Medium
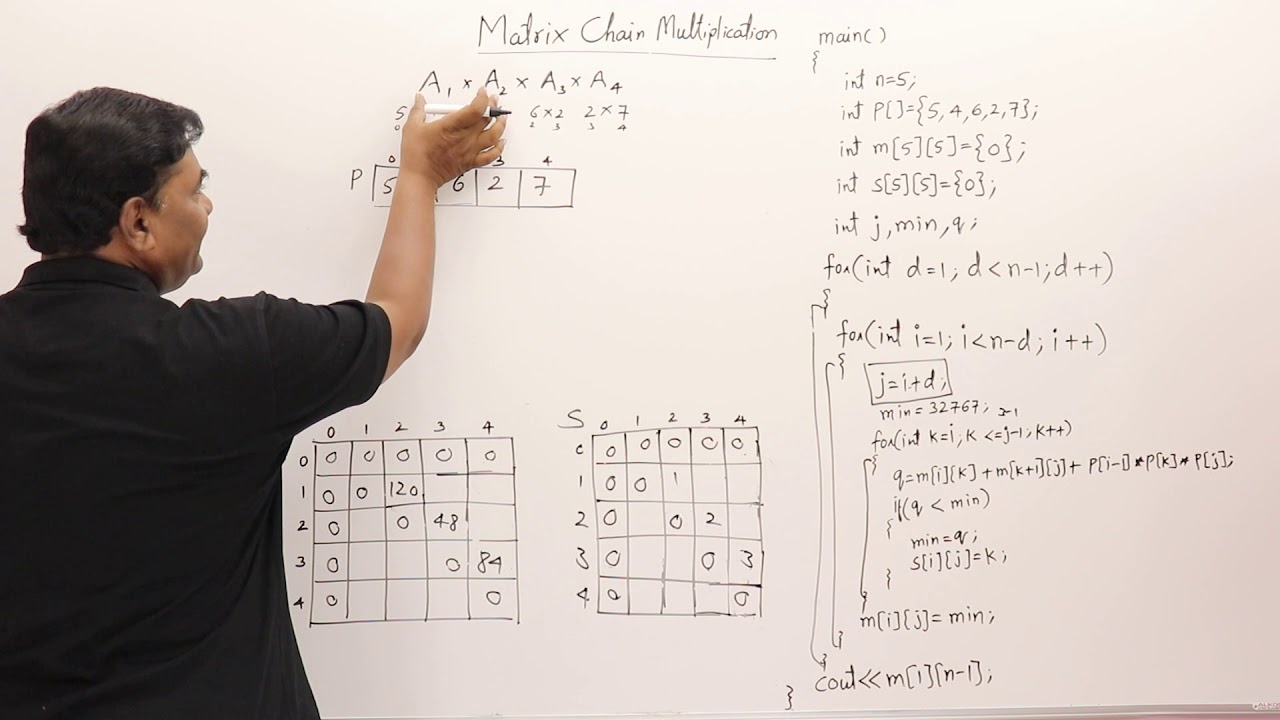
4 3 1 Matrix Chain Multiplication Program Dynamic Programming Youtube

4 3 Matrix Chain Multiplication Dynamic Programming Youtube

Unit 4 Dynamic Programming Ppt Video Online Download

Matrix Chain Multiplication Dynamic Programming Youtube

Massive Algorithms Matrix Chain Multiplication

Unit 4 Dynamic Programming Ppt Video Online Download

Matrix Chain Multiplication Using Dynamic Programming By Chetan More Medium

Matrix Chain Multiplication Matrix Chain Multiplication Is An By Vaibhavi Maradiya Medium

Matrix Chain Multiplication Problem Using Dynamic Programming Part 2 Youtube


