Matrix Chain Multiplication Example Step By Step
Matrix B left number of columns 3. ABCD - This is a 2x4 multiplied by a 4x1 so 2x4x1 8 multiplications plus whatever work it will take to multiply BCD.
E E to have a product the number of columns of left matrix B must equal the number of rows of right matrix E.

Matrix chain multiplication example step by step. Step3 for i in range 2 to N-1. Matrix E right number of rows 3. C1 Display every element to take into account Aik Bkj Prepare the addition in the iteration s s Aik Bkj.
The Chain Matrix Multiplication Problem is an example of a non-trivial dynamic programming problem. Holds the number of scalar multiplication needed for int i1. Initialize for k i to j 1 do try all possible splits costRec-Matrix-Chainp i k Rec-Matrix-Chainp k 1 j pi 1pkpj.
ABCD - This is a 2x2 multiplied by a 2x1. Let the input 4 matrices be A B C and D. We need to compute M ij 0 i j 5.
That is 5 Example 5. We know M i i 0 for all i. Set to infinity for int ki.
Matrix Chain Multiplication Consider the case multiplying these 4 matrices. Algorithm For Matrix Chain Multiplication Step1 Create a dp matrix and set all values with a big valueINFINITY. For multiplication with 1 matrix cost is 0 for int length2.
We are given the sequence 4 10 3 12 20 and 7. The matrices have size 4 x 10 10 x 3 3 x 12 12 x 20 20 x 7. Step2 for i in range 1 to N-1.
The m and s table computed by MATRIX- CHAIN-ORDER for n6. Vary each column of matrix A and row of matrix B for k 1. K is used to know current column number of A and row number of B to be multiplied static int i 0 j 0 k 0.
Let us proceed with working away from the diagonal. In this article I break down the problem in. N length p-1 Where n is the total number of elements And length p 5 n 5 - 1 4 n 4 Now we construct two tables m and s.
Example A 1 is 10 by 100 matrix A 2 is 100 by 5 matrix A 3 is 5 by 50 matrix A 4 is 50 by 1 matrix A 1A 2A 3A 4 is a 10 by 1 matrix. K store cost per multiplications int. P 10 20 30 40 30 Output.
P 10 20 30 40 30 Output. Place them side by side. Example of Finding the Multiplication Sequence.
Void multiplyMatrixRecint row1 int col1 int AMAX int row2 int col2 int BMAX int CMAX Note that below variables are static i and j are used to know current cell of result matrix C. Please like and subscribe. Matrix Chain MultiplicationDynamic ProgrammingPATREON.
For the matrix-chain multiplication problem we can perform this step as follows. Int matOrderint array int n int minMulnn. End Assign the total of the appropriate element to the final matrix Cij s end end Compare our result with a multiplication by Matlab AB.
Rec-Matrix-Chainarray p int i int j if i j mi i 0. For any optimal multiplication sequence at the last step youare multiplyingtwo matrices and for some. 4Constructing an Optimal Solution.
I int j ilength-1. The minimum number of multiplications are obtained by putting parenthesis in following way A BCD -- 203010 402010 401030 Input. Length find the chain length starting from 2 for int i1.
I minMulii 0. Let the input 4 matrices. Basic case else mi j infinity.
M 25 min m 22m 35p1p2p50250035 15 20 13000 m 23m 45p1p3p52625100035 5 207125 m 24m 55p1p4p54375035 10 20 11374 7125. For convenience let us adopt the notation Aijfor the matrix that results from evaluating the product AiAi 1Aj. Now these are the steps.
The matrix multiplication optimization step by step. Example of Matrix Chain Multiplication. There are following examples.
The Chain Matrix Multiplication Problem Given dimensions corresponding to matr 5 5 5 ix sequence. 30000 There are 4 matrices of dimensions 10x20 20x30 30x40 and 40x30. A 1A 2A 3A 4 A 34 A 3A 4 250 mults result is 5 by 1 A 24 A 2A 34 500 mults result is 100 by 1 A 14 A 1A 24 1000 mults result is 10 by 1 Total is 1750 A 1A 2A 3A 4 A 12 A 1A.
30000 There are 4 matrices of dimensions 10x20 20x30 30x40 and 40x30. Length of array P number of elements in P length p 5 From step 3 Follow the steps in Algorithm in Sequence According to Step 1 of Algorithm Matrix-Chain-Order Step 1. We compute the optimal solution for the product of 2 matrices.
For j in range 1 to N-i1. Recursive code for Matrix Multiplication include const int MAX 100. This project contains examples of programs optimization.
The minimum number of multiplications are obtained by putting parenthesis in following way A BCD -- 203010 402010 401030 Input. Since this is the case then it is okay to multiply them together. Include using namespace std.
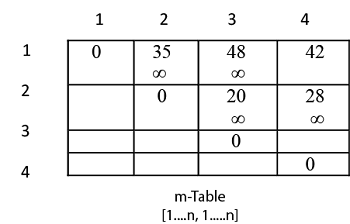
Matrix Chain Multiplication Algorithm Javatpoint
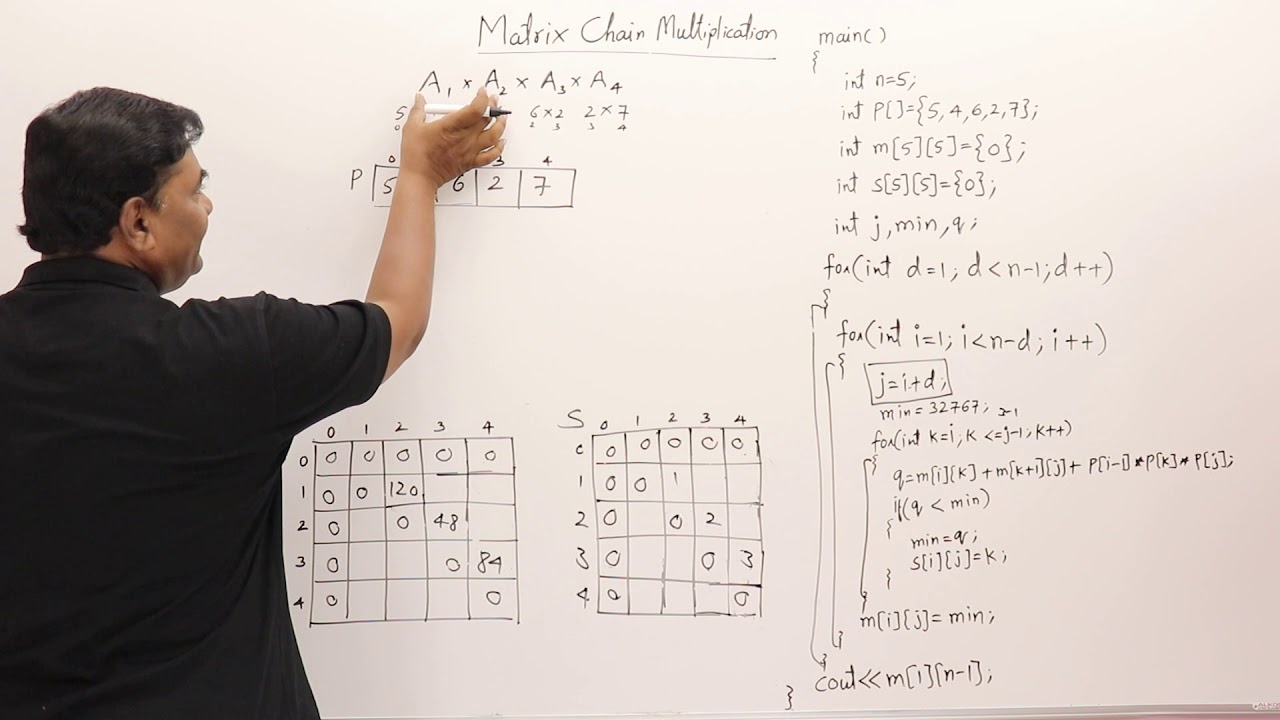
4 3 1 Matrix Chain Multiplication Program Dynamic Programming Youtube
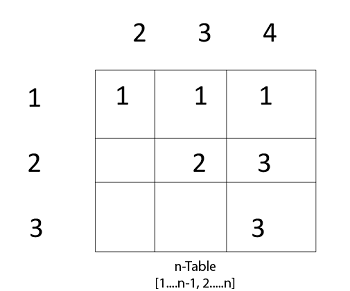
Matrix Chain Multiplication Algorithm Javatpoint

Matrix Chain Multiplication Dynamic Programming Youtube

Matrix Chain Multiplication Using Dynamic Programming By Chetan More Medium
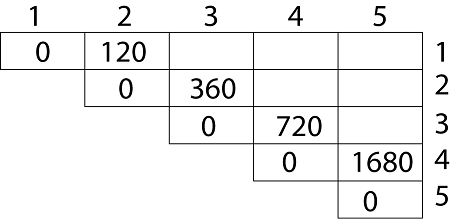
Matrix Chain Multiplication Using Dynamic Programming By Chetan More Medium
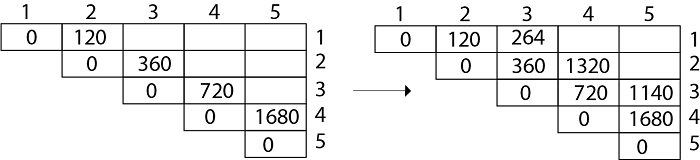
Matrix Chain Multiplication Using Dynamic Programming By Chetan More Medium
Dynamic Programming Sample Problem Matrix Chain Multiplication Review Ics 311

Matrix Chain Multiplication Problem Using Dynamic Programming Part 2 Youtube
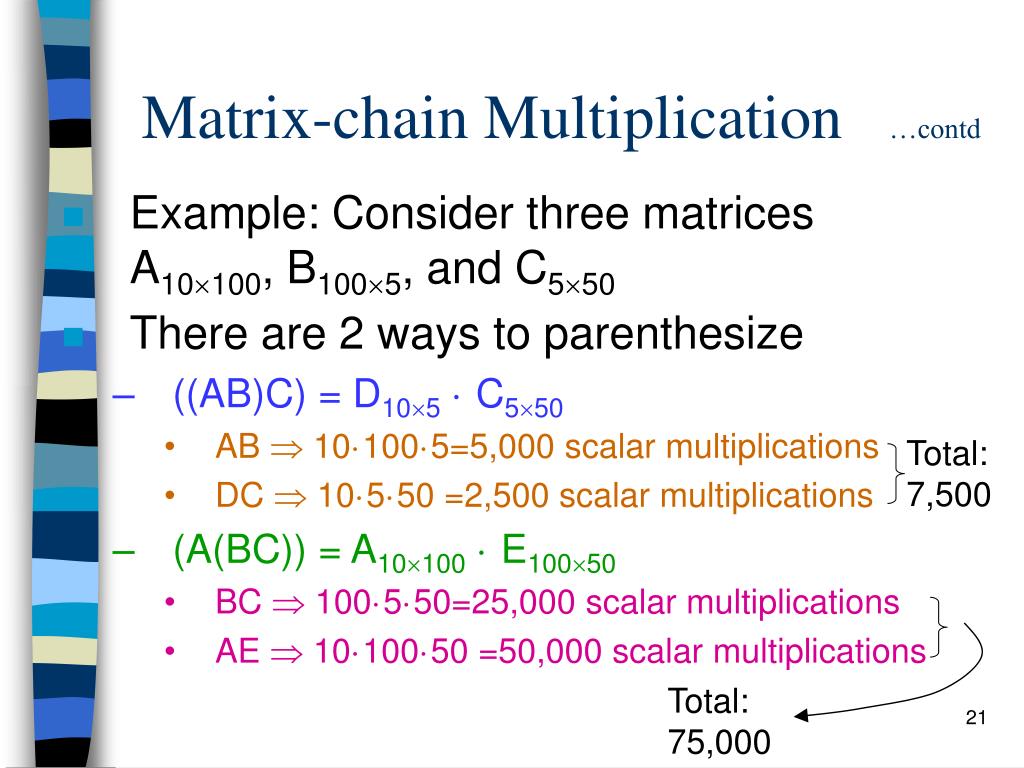
Ppt Dynamic Programming Powerpoint Presentation Free Download Id 4708061

4 3 Matrix Chain Multiplication Dynamic Programming Youtube
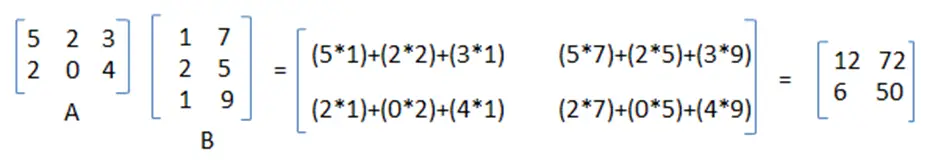
Matrix Chain Multiplication In C And C The Crazy Programmer




