Fast Algorithm For Matrix Multiplication
In our main algorithm we perform c independent trials where in each trial we randomly sample an element of 12ldots n with an appropriate probability distribution cal P on 12ldots n. Suppose A and B which are mtimes n and ntimes p respectively are the two input matrices.

Time Complexity Of Matrix Multiplication In Big Align Computer Science Stack Exchange
The operation of matrix multiplication is reformulated as a convolution which is implemented using.
Fast algorithm for matrix multiplication. Matrix mult_std matrix const a matrix const b. Fast and stable matrix multiplication p1344. And to answer why the original method is 4 times faster we would need to see the original method.
Two Fast Algorithms for Sparse Matrices. For maximum speed the designs are based upon a 0. The designs are then compared on the basis of delay power and area.
Viewed 868 times -2 Recently I have learned about both the Strassen algorithm and the CoppersmithWinograd algorithm independently according to the material Ive used the latter is the asymptotically fastest known matrix multiplication algorithm until 2010. The first to be discovered was Strassens algorithm devised by Volker Strassen in 1969 and often referred to as fast matrix multiplication. Simple Matrix Multiplication MethodDivide and Conquer MethodStrassens Matrix Multiplication MethodPATREON.
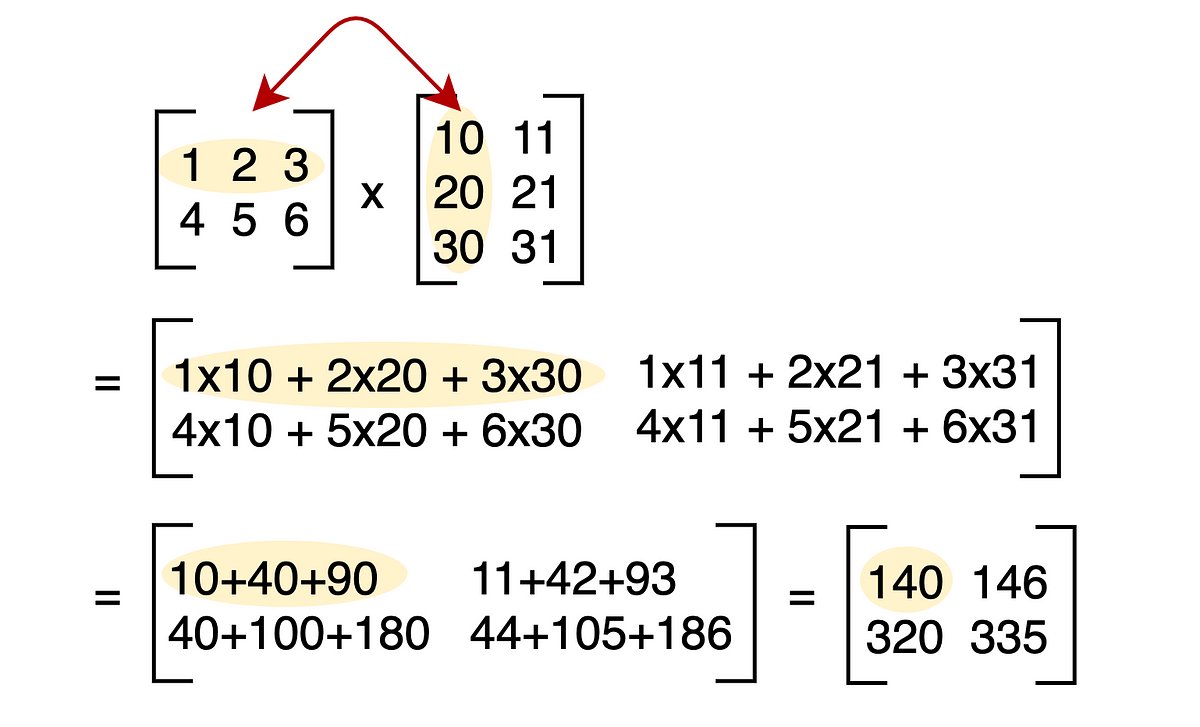
The product C AB is defined as follows. The optimal number of field operations needed to multiply two square n n matrices up to constant factors is still unknown. Strassens algo-rithm is an improvement over the naive algorithm in the case of multiplying two 22 matrices.
SIAM News Nov 2005 by Sara Robinson. Found groups with subsets beating the sum of the cubes and satisfying the triple product property. C ij n k1 a ikb kj for 1 i j n.
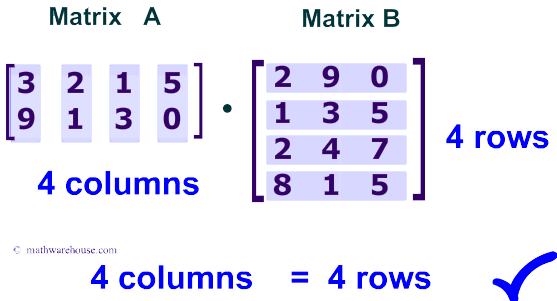
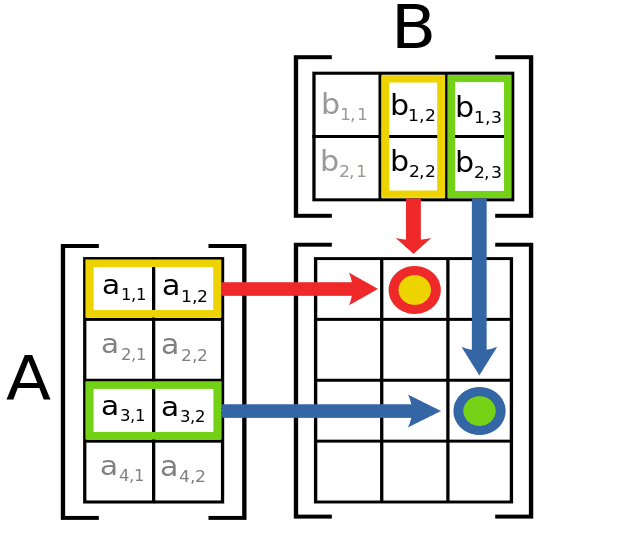
9 rows In linear algebra the Strassen algorithm named after Volker Strassen is an algorithm for. Time complexity of multiplication can be further improved using another Divide and Conquer algorithm fast Fourier transform. Obviously this algorithm takes On3 time if m n p.
THE NAıVE MATRIX MULTIPLICATION ALGORITHM. As It can multiply two n n matrices in 0 n2375477 time. The algorithm above gives the following recursive equation Nn3Nn12 1On and N27.
Reid Ed Academic Press London and New York pp. This is a major open question in theoretical computer science. You can think of the matrix multiplication problem as a much harder analogue of these problems where analogous solutions would rely on complicated group-theoretic constructions.
Highlights include Sch onhages asymptotic sum inequality 8 Strassens laser method 12 and the CoppersmithWinograd algorithm 4. The algorithms developed in this thesis make possible 53x53 mul-. We will soon be discussing fast Fourier transform as a separate post.
In this paper we devise two algorithms for the matrix multiplication problem. Sparse matrix algorithms and their relation to problem classes and computer architecture. Fast algorithms for matrix multiplication using pseudo-number-theoretic transforms Abstract.
Time complexity of the above solution is O n log23 O n 159. Several algorithms with OnX running time where 2 x 3 have been proposed 5. Begingroup If you havent done so already you might start by reading up on the algorithms for fast integer multiplication and fast Fourier transform.
The naıve matrix multiplication algorithm uses this definition. A theory of fast algorithms for matrix multiplication has been developed. This procedure will be called the standard matrix multiplication algorithm.
We provide a novel approach to the design of fast algorithms for matrix multiplication. Nn denote the number of arithmetic operations that the above algorithm needs to multiply polynomial of degree n. Plication algorithm and state the performance of existing fast matrix multiplication algorithms.
Pass the parameters by const reference to start with. 3 rows We provide a new hybrid parallel algorithm for shared-memory fast matrix multiplication. Multiplication and Permuted Transposition.
In Large Sparse Sets of Lnear Equations J. Fast matrix multiplication is still an open problem but implementation of existing algorithms 5 is a more com-mon area of development than the design of new algorithms 6. 6 BiCMOS process using emitter coupled logic ECL.
Let A and B be two n n matrices. To give you more details we need to know the details of the other methods used. Booth encoded non-Booth encoded and the new extended Booth algorithms.
Algorithm this question has captured the imagination of computer scientists. Group-theoretic algorithms for matrix multiplication FOCS Proceedings 2005. A trivial lower bound on the time complexity for multiplying two general n X n matrices is Ûn2.
Similarly to the analysis of Strassens algorithm.
Matrix Multiplication In C Applying Transformations To Images Codeproject

A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science

Performing Convolution By Matrix Multiplication F Is Set To 3 In This Download Scientific Diagram

Sparse Matrix Multiplication Description By Glyn Liu Medium

Communication Costs Of Strassen S Matrix Multiplication February 2014 Communications Of The Acm

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
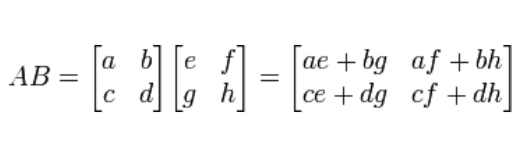
Breakthrough Faster Matrix Multiply

2 9 Strassens Matrix Multiplication Youtube

A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science

Matrix Multiplication With 1 Mapreduce Step Geeksforgeeks

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
Introduction To Matrices And Matrix Arithmetic For Machine Learning

Pseudocode For Matrix Multiplication Download Scientific Diagram





