Unitary Matrix Rotation Matrices
Noting that any identity matrix is a rotation matrix and that matrix multiplication is associative we may summarize all these properties by saying that the n n rotation matrices form a group which for n 2 is non-abelian called a special orthogonal group and denoted by SOn SOnR SO n or SO n R the group of n n rotation. R 1 2 cos.

4 Given The Matrix Li 0 0 0 1 This Is One Of The Chegg Com
Solution Since AA we conclude that A Therefore 5 A21.

Unitary matrix rotation matrices. References 1 BR Desai. A is a unitary matrix. It occurred to me after the fact that the Lorentz boost is not Unitary.
A2 0 where A2 is n 1 n1 Since it is unitary it must have orthogonal columns by Theorem 412. In general a 2X2 matrix represents a rotation in three dimensions. Furthermore detU 1 detA2 detA 2 1 so Uis unimodular.
Structure of unitary matrices is characterized by the following theorem. Again using the arccos. The eigenvalues thus chosen are random variables.
Two-level unitary matrix is a unitary matrix obtained from an identity matrix by changing a 22 principal submatrix. A simple way to verify a matrixs unitarity is to check the equation. Q0 iq1 q2 iq3 q2 iq3 q0 iq1.
θ H θ 0 γ z γ y γ z 0 γ x γ y γ x 0 where γ x 2 γ y 2 γ z 2 1 γ x γ y γ z is a unit vector defining the axis of rotation as you can prove by finding the eigenvectors and values of H and showing that this vector is the eigenvector corresponding to an eigenvalue of 0 therefore the exponential of exp. Any unitary matrix U n can be represented as follows. This kind of matrices are called unitary matrices denoted as U.
If UyU 1 then we have trA0 trAand U is a rotation. Rθe0 cosθ sinθ and Rθe1 sinθ cosθ. We now write U 1 detA A2 1 detA a0ia2 1 detA a2 02ia0aj aj2 a2 0 j aj2 a 2 0 jaj2 2a0jaj a0 jaj2 ia where a ajaj.
UdaggerUUUdaggerI text Eq1 where Udagger U dagger is the conjugate transpose of U which means to take the transpose of U and then take the complex conjugate of each of the transpose entries. If U is orthogonal then det U is real and therefore det U 1 As a simple example the reader can verify that det U 1 for the rotation matrix in Example 81. The q above can be written as a 2 2 unitary matrix.
If U is a unitary matrix then 1 detUhU det Uhdet U det Udet U det U2 so that det U 1. Makes the matrix P1 with all these vectors as columns a unitary matrix. In other words take identity matrix select distinct indices and replace elements such that remains unitary youll get two-level unitary matrix.
The distance between rotations represented by rotation matrices P and Q is the angle of the difference rotation represented by the rotation matrix R P Q. 13 The form of rotation matrices WenowfindthegeneralformofanSU2 transformation. 2 θ arccos.
StartingfromaninfinitesimalrotationU 1 werequire UUy 1 1 1 y 1. U n H n Θ H n where H n is a unitary matrix Θ n exp i θ p δ p l and the expiθ p are the eigenvalues of U n. The group homomorphism from SU2 to SO3 has a two element kernel and this corresponds to the am-biguity in the choice of rotation axis in the logarithmic.
A matrix A is unitary if and only if the corresponding linear map v A v is an isometry meaning that it preserves lengths and distances. If you may remember I concluded my last post with an outlook on learning unitary matrices with qgradThis post goes into the details of what unitary learning is and how one can implement unitary learning in qgrad. C n C m is a linear transformation and A A is the matrix that represents it then the j j th column of A A aj a j equals Lej.
EXAMPLE 2 A Unitary Matrix Show that the following matrix is unitary. L e j. 5 1 2 3 1 1 i 1 2 i 1 2 i.
6 SU2 provides a double-covering of SO3. θ n 2π. Unitary matrices matrices A are invertible matrices that have property that A T A 1.
In fact they are diagonalizable by special orthogonal matrices rotations S O n because we can always includeremove a reflection with negative determinant. Unitary transformations are utterly important in quantum computing primarily because they preserve the norm of the vectors and thus keep the quantum states normalized. However it has the form B1 λα1.
Recall that if LCn Cm L. In other words A v v. That is each rotation matrix in SO3 corresponds to two members of SU2.
We arrange the arguments of the eigenvalues in nonincreasing order 0 θ 1 θ 2. It is well-known that real symmetric n n matrices are diagonalizable by orthogonal matrices O n. The fact that the eigenvalues are not a purely complex phase term like those of the rotation is actually a good hint that looking at how to characterize the eigenvalues of a unitary matrix can be used to show that the matrix is Hermitian.
The Lie group S O n of n -dimensional rotations are. The complex 2-dimensional matrices with UyU 1 areunitaryandsincewehavealreadyaskedforunitdeterminanttherotationgroupisSU2. Unitary Matrices Recall that a real matrix A is orthogonal if and only if In the complex system matrices having the property that are more useful and we call such matrices unitary.
This leads to a very neat geometric characterisation. Therefore B1 P1UP is also unitary. Find the axis and angle of rotation appropriate for Uin terms of a0a1a2and a3.
Let us compute the matrix that represents the rotation through an angle θ. We can retrieve the angle of the difference rotation from the trace of R.

C Prove That The Eigenvalues Of A Unitary Matrix U Chegg Com
This Part Focuses On Orthonormal Rotation Matrices Chegg Com
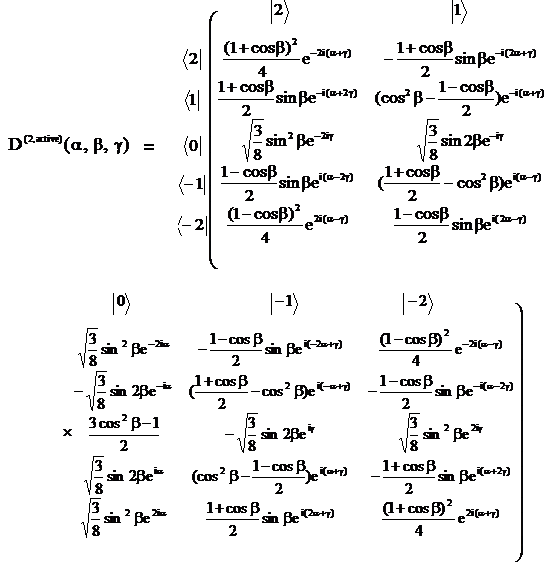
Wigner Rotation Matrices For Second Rank Spherical Tensor

This Part Focuses On Orthonormal Rotation Matrices Chegg Com
Matrix Rotations And Transformations Matlab Simulink Example

How To Find The Rotation Matrices For Robotic Arms Automatic Addison

Rotating Points Using Rotation Matrices Youtube
Orthogonal Matrices Linear Algebra

Orthogonal Matrix An Overview Sciencedirect Topics

Chapter 3 Linear Algebra February 26 Matrices 3

Matrix Matrices An Overview Sciencedirect Topics
Define The Rotation Operator With Angle Over The Chegg Com

Thanksci Vi Gauge Symmetries Classical Physics Wave Function Mechanical Wave
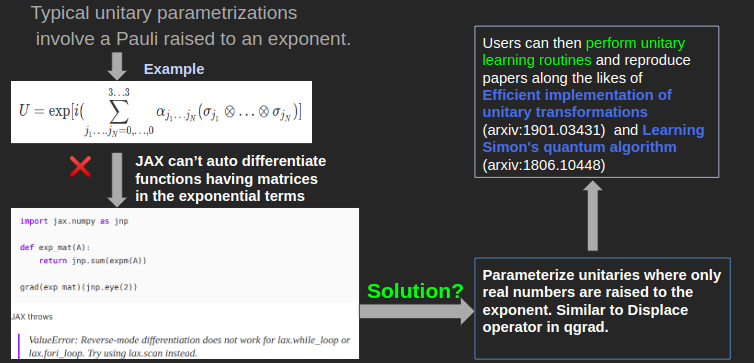
Learning Unitary Matrices Asad Raza
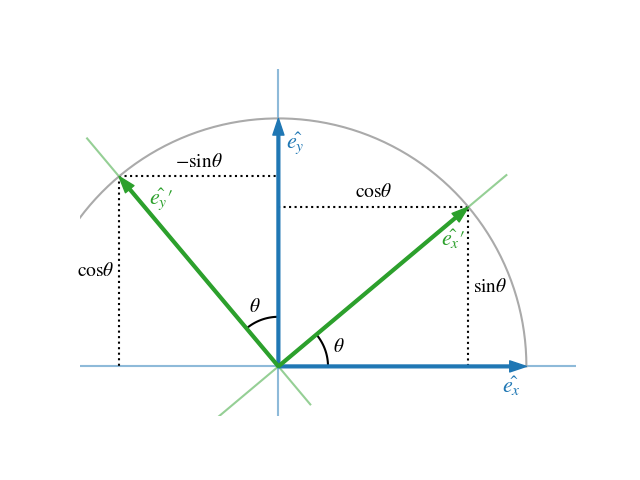
Creating A Rotation Matrix In Numpy

8 The Pauli Spin Matrices Are And 10 S2 Chegg Com





