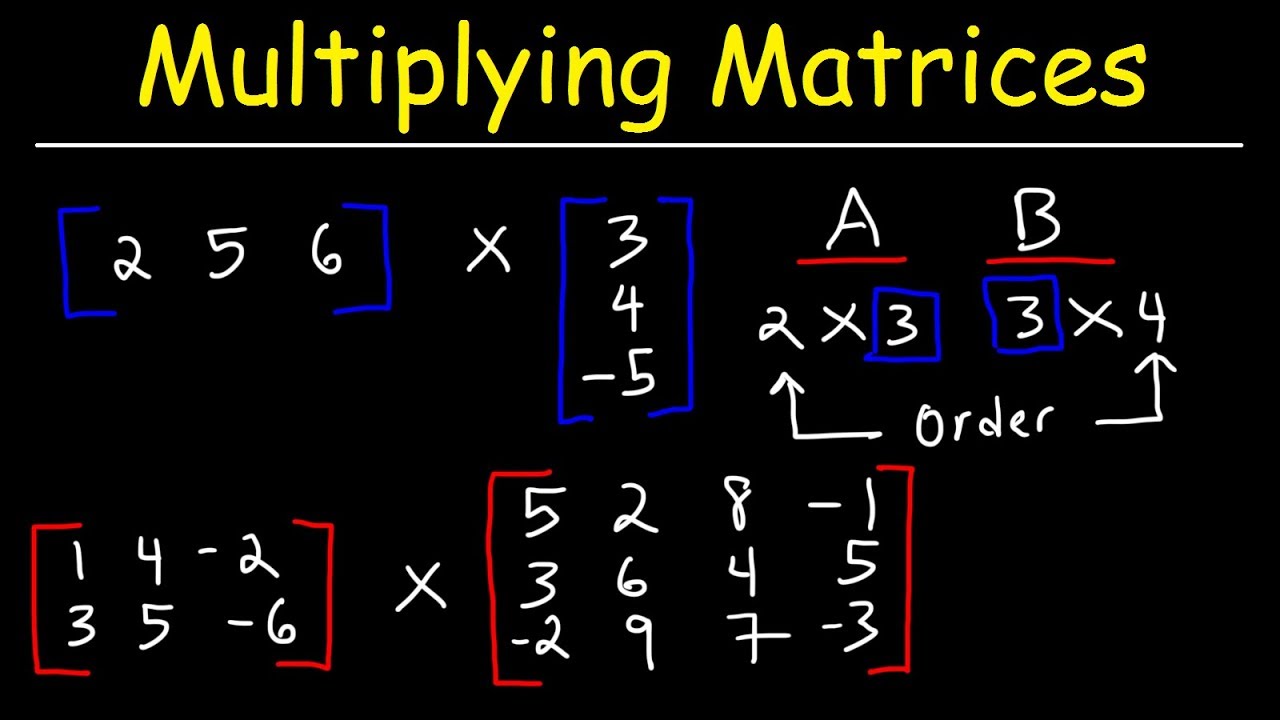
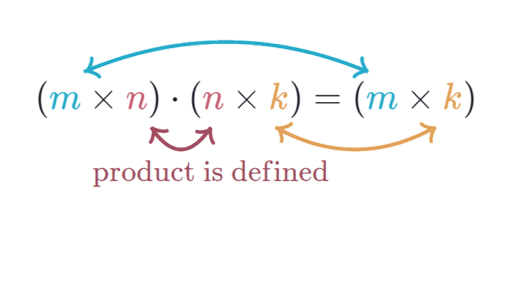Matrix Multiplication Rules Rows Columns

A i n b n j. Yielding a total of three matrix multiplications.

Pin On Mrs Algebra

If I multiply a column by a row--should we just do one.

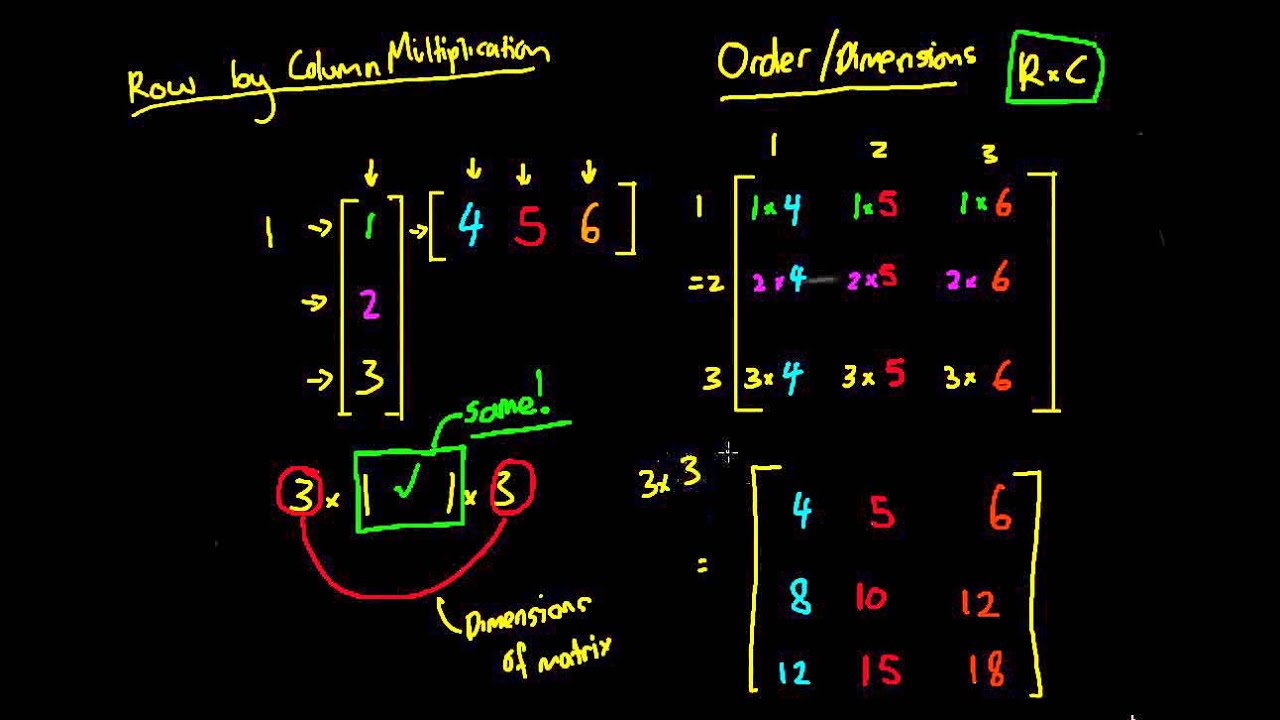
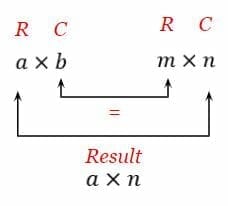
Matrix multiplication rules rows columns. A B c i j where c i j a i 1 b 1 j a i 2 b 2 j. Recall that the size of a matrix is the number of rows by the number of columns. Make sure that the the number of columns in the 1 st one equals the number of rows in the 2 nd one.

If A a i j is an m n matrix and B b i j is an n p matrix the product A B is an m p matrix. 10 1 4 7 13 2 5 8 15 3 6 9 which is one column of A B. With multi-matrix multiplication the order of individual multiplication operations does not matter and hence does not yield different results.

The extension of the concept of matrix multiplication to matricesA B in whichAhas more than one row andBhas more than onecolumn is now possible. 1 4 7 10 11 12 we get a matrix. That product there--I mean when Im just following the rules of matrix multiplication those rules are just looking like--kind of petite kind of small because the rows here are so short and the.

Columns come second so second matrix provide column numbers. That is AB is typically not equal to BA. Code A 1 2 3.

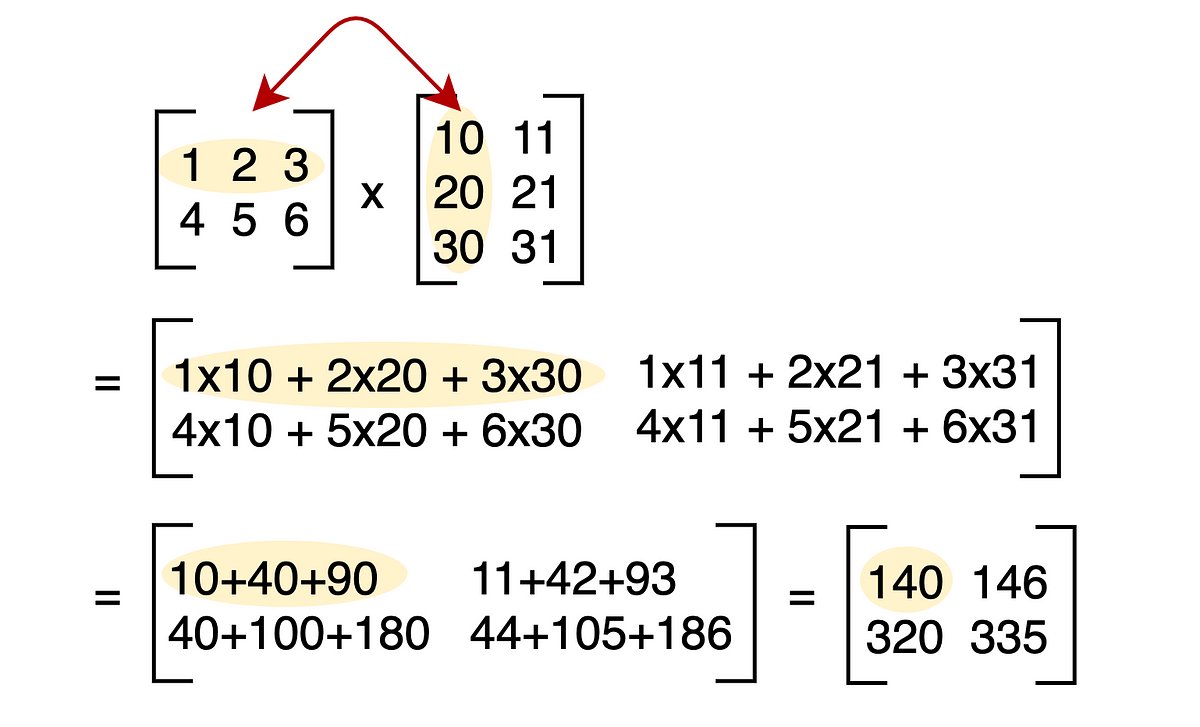
Each of the 3 matrices a i b i T summed together gives us A B. To multiply any two matrices we need to do the dot product of rows and columns. I get a full-sized matrix.

Rows come first so first matrix provides row numbers. If at least one input is scalar then AB is equivalent to AB and is commutative. Regular matrix multiplication row by row multiplication and column by column multiplication.

The product matrixABwill have the samenumber of columns as Band each column is obtained by taking theproduct of Awith each column of B in turn as shown belowLetA4 2. The rule for matrix multiplication however is that two matrices can be multiplied only when the number of columns in the first equals the number of rows in the second that is the inner dimensions are the same n for an m n-matrix times an n p-matrix resulting in an m p-matrix. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators.

This is also known as the dot product. Lets first understand about matrix dot product. You can only multiply two matrices if their dimensions are compatible which means the number of columns in the first matrix is the same as the number of rows in the second matrix.

The product of these two matrices lets call it C is found by multiplying the entries in the first row of column A by the entries in the first column of B and summing them together. As you can see the sizes of the matrices do not have to be the same you just need the middle two numbers to match when you write the sizes side by side. The order of the matrices is important.

An important property of matrix multiplication operation is that it is Associative. If the first matrix has a dimension of a times b and the second matrixs dimension is m times n for matrix multiplication to be defined the number of columns of the first matrix b must equal the number of rows of the second matrix m. The resulting matrix will have rows equal to the number of rows in A and columns equal to the number of columns in C.

For nonscalar A and B the number of columns of A must equal the number of rows of B. Before going to the step-by-step process of matrix multiplication. Let me take the column two three four times the row one six.

The matrices above were 2 x 2 since they each had 2 rows and 2 columns. Multiply the elements of each row of the first matrix by the elements of each column in the second matrix. If however we multiply each column of A by each row of B eg.

Matrix multiplication is not universally commutative for nonscalar inputs. This are just simple rules to help you remember how to do the calculations. Otherwise the product is undefined.

This single value becomes the entry in the first row first column of matrix C. Normally we would multiply each column of B by A and get a linear combination of A eg. So to do the dot product of 123.

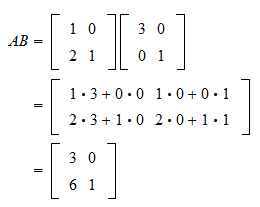
Matrix Multiplication And Linear Combinations

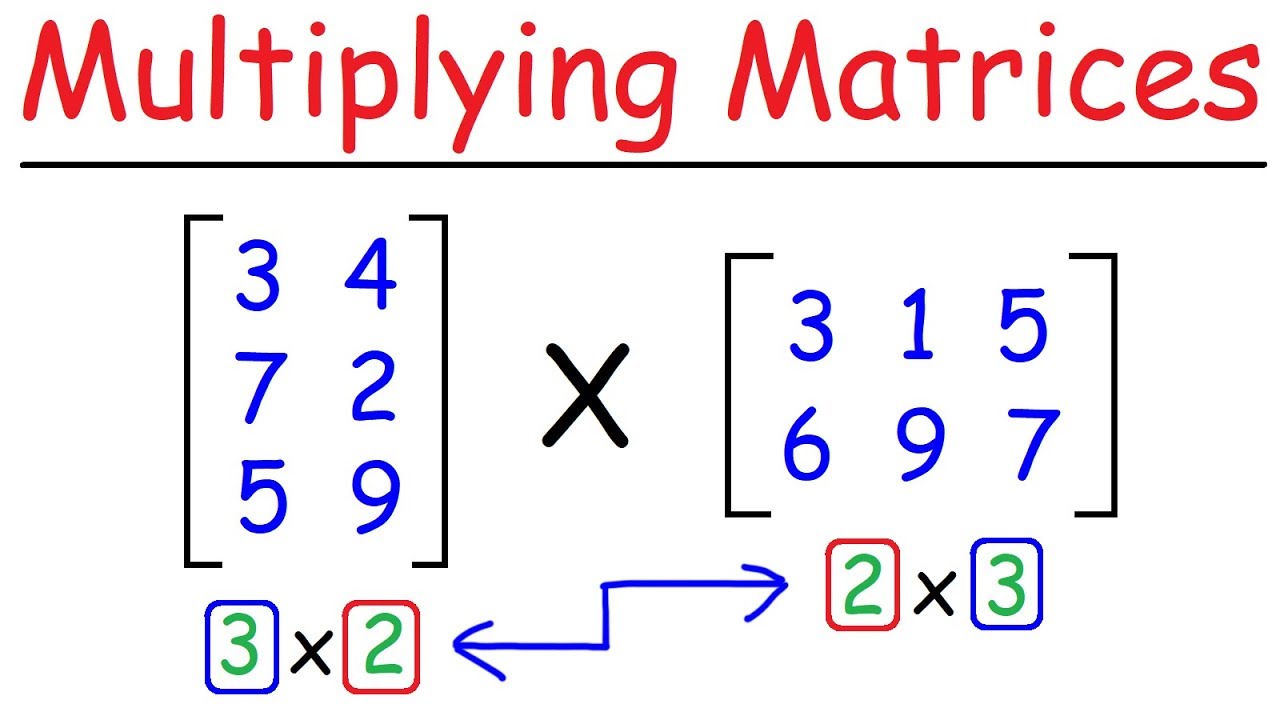
How To Multiply Matrices Quick Easy Youtube

Multiplying Matrices Youtube

Matrix Multiplication Column By Row Youtube

Matrix Multiplication Made Easy

Raw Material

Matrix Multiplication Review

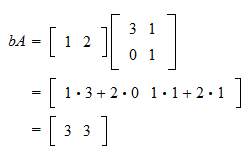
Matrix Multiplication And Linear Combinations

A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science

Matrix Multiplication Explanation Examples

Matrix Multiplication Review

How To Multiply Matrices Matrices Math Learning Mathematics Math Formulas

Matrix Multiplication In C Applying Transformations To Images

Misconceptions When Multiply 2 Matrices The First Matrix S Column Needs To Match The Value Of The Second Matrix S Row In O Matrices Math The One Matrix Matrix

Pin On Mathematics

Pin On High School Math

Matrix Multiplication Dimensions Article Khan Academy

Mega Matrix Multiplication

Pin On Colleges