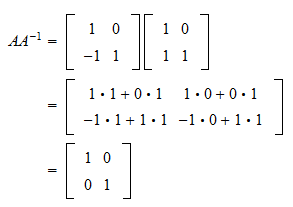Matrices Invertible Rank

11 Aug, 2021

Remember that the rank of a matrix is the dimension of the linear space spanned by its columns or rows. The rank of a matrix cannot exceed more than the number of its rows or.

Inverse Matrix Determinants

What is known about the relationships between the ranks of A 21 and B 21.

Matrices invertible rank. An n-by-m matrix B such that AB I. P2 R P R T f x f x 2f - f x B 1 22 3. 1 3 0 A0 0 5 3 10 0 4.

If the rank of a 5 x 6 matrix Q is 4 then which one of the following statements is correct. For the given linear transformation T find T the rank of T the inverse of Te and use T to construct T-1 T. Note that A is an invertible matrix if and only if its rank is 3.

Let A 1. If A is full rank it is surjective column space span R n and injective x y A x A y therefore it is invertible. Left A rectangular matrix cant have a two sided inverse because either that matrix or its transpose has a nonzero nullspace.

A 1 1 d e t A e i f h c h b i b f c e f g d i a i c g c d a f d h g e b g a h a e b d and since the determinant of a matrix without full rank is 0 you have that 1 d e t A 1 0 and thus the inverse does not exist - Share. A is m x n full matrix with m n and I is an identity matrix. We call C a left inverse of A1 We say that A is right invertible if there exists an n m matrix D such that AD I m.

K2 3k 2 k 1k 2 0. Let matrix A ATA-1 AT then which one of the following statements is true. Express the matrix A and its inverse A-1 as a product of elementary matrices.

Well then if you a non zero column vector which you correctly declared has a rank. The rank of the matrix refers to the number of linearly independent rows or columns in the matrix. If A has rank m then it has a right inverse.

For example if either A 11 or A 22 is invertible then it can be easily shown using the block inverse formula that the ranks are equal. Two matrices A and B are given below. Answered Jan 22 14 at 939.

Rank of a Matrix Definition. A square matrix that is not invertible is called singular or degenerate. Where is the vector of coefficients of the linear combination.

The fact that AT A is invertible when A has full column rank was central to our discussion of least squares. We say that A is left invertible if there exists an n m matrix C such that CA I n. We are going to prove that the ranks of and are equal because the spaces generated by their columns coincide.

E 1s I But E 1i are also invertible as I so A is invertible as well. Express the invertible matrix below as a product of elementary matrices. ρA is used to denote the rank of matrix A.

E2E1A I and so A E 11. Prove that an m xn matrix A has rank 0 if and only if A is the zero matrix. A matrix is said to be of rank zero when all of its elements become zero.

The rank of the matrix is. How to think about linear systems of equations geometricallyHelp fund future projects. Therefore the 3 3 -entry of the last matrix must be nonzero.

The rank of the matrix is the dimension of the vector space obtained by its columns. Right inverse If A has full row rank then r m. B B 11 B 12 B 21 B 22 and shape of B 11 is same as A 11.

If rankA n then A is an equivalent matrix to In n. De nition 1. Click here if solved 35.

And to find the dimension of a row space one must put the matrix into echelon form and grab the remaining non zero rows. Let A A 11 A 12 A 21 A 22 be an invertible matrix where A 11 is square. We call D a right inverse of A2 We say that A is invertible if A is both left invertible and right invertible.

Note that AA1 is an m by m matrix which only equals the identity if m n. Denote by the space generated by the columns of Any vector can be written as a linear combination of the columns of. If A is invertible k e r A then A is full rank.

This means that there are some elementary matrices E1 E2 Es such that Es. Note that the rank of a matrix is equal to the dimension of its row space so the rank of a 1x3 should also be the row space of the 1x3. Let A be an m n matrix.

It follows that the matrix A is invertible for any k except k 1 2.

Solved True Or False If A Is An M X N Matrix And A A Is Chegg Com