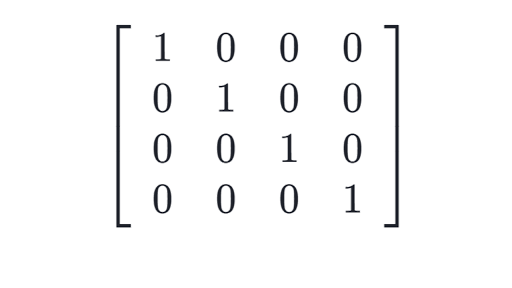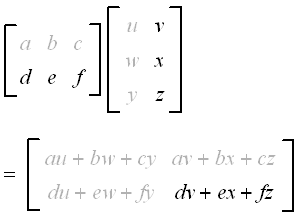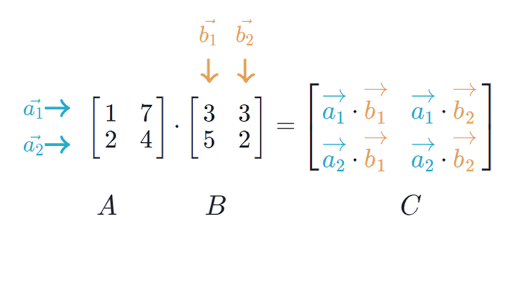Matrix Times Matrix Transpose Equals Identity
RRI If yes then the matrix is orthogonal. Matrix times its transpose equals minus identity.
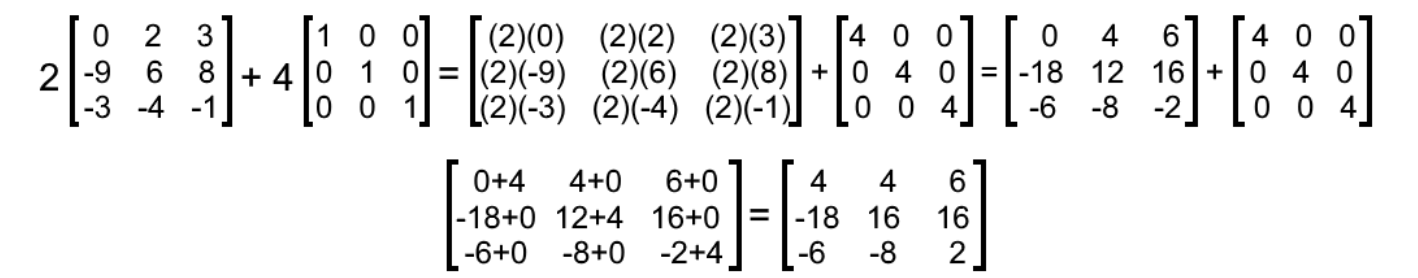
What Is An Identity Matrix Studypug
You can take any real-valued square orthogonal matrix A eg.
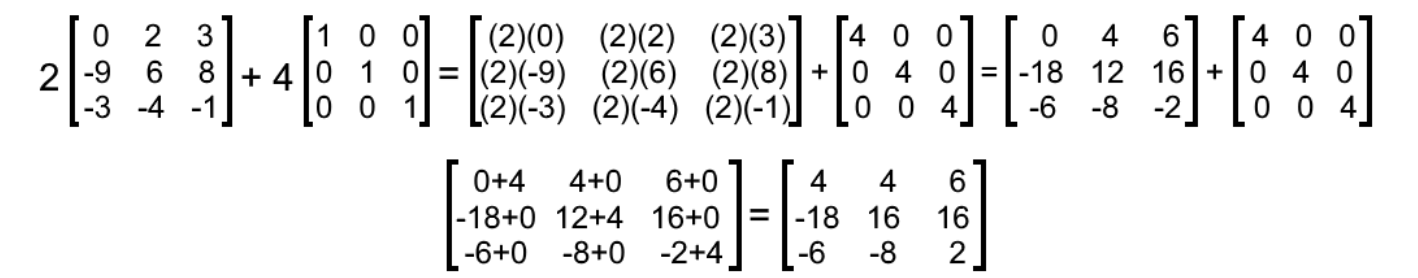
Matrix times matrix transpose equals identity. The matrix on the right side equals its inverse. What is a matrix inverse. Then multiplying A by i 1 will give you what you want.
The left-side matrix is the initial matrix and the right-side matrix is an identity matrix. By the definition of identity matrix we have. By the definition of a transpose I T is an n n matrix such that I i j T I j i.
That is the beauty of having properties like associative. What is the identity matrix. B b conjg transpose a end function ct function identity n result b.
Definition The transpose of an m x n matrix A is the n x m matrix AT obtained by interchanging rows and columns of A Definition A square matrix A is symmetric if AT A. N real dimension nn. You wont end up at the same conclusion.
AB is just a matrix so we can use the rule we developed for the transpose of the product to two matrices to get ABCT CT ABT CT BT AT. B B B T B 1 2 B T B 1 2 Least Squares methods employing a matrix multiplied with its transpose are also very useful with Automated Balancing of. Ie AT ij A ji ij.
I i j 1 if i j 0 if i j. Can someone look at my code and tell me why this would be so. A B T A T B T Transpose of a product.
Return identity matrix integer intent in. What is a scalar. If i j then I i j T I i i T I i i 1.
Carry out matrix multiplication. Especially the following formula over there leaves no doubt that a matrix multiplied with its transpose IS something special. Return the conjugate transpose of a matrix complex dimension intent in.
Comment on Dhoomketus post Its only true if A is a square matrix. For matrix multiplication the number of columns in the first matrix must be equal to the number of rows in the second matrix. The transpose of a matrix times a scalar k is equal to the constant times the transpose of the matrix.
Show that there exists a matrix that when pre-multiplied by the design matrix yields the identity matrix. Let us use the fact that matrix multiplication is associative that is ABCA BC. The number 1 is called the multiplicative identity for real numbers.
The resulting matrix known as the matrix product has the number of rows of the first and the number of columns of the second matrix. For real matrices the conjugate transpose is just the transpose. KA T kA T Transpose of a sum.
I have most been using isequal but it keeps yielding false. If a matrix is multiplied by a constant and its transpose is taken then the matrix obtained is equal to transpose of original matrix multiplied by that constant. Reflection rotation any distance preserving linear transformation and for this matrix A you will have by definition A T A I.
Matrix transpose AT 15 33 52 21 A 1352 532 1 Example Transpose operation can be viewed as flipping entries about the diagonal. You can prove it if you follow the same process for A x A-transpose. There is a matrix which is a multiplicative identity for matricesthe identity matrix.
This technique involves two adjacent matrices. That is kA kA where k is a constant. Now suppose that i j.
Transpose of a scalar multiple. Hot Network Questions RMSE vs MSE loss function - the optimization solutions are equivalent. The identity property of multiplication states that when 1 is multiplied by any real number the number does not change.
Function ct a result b. A complex dimension size a 1 size a 1. In mathematics the conjugate transpose or Hermitian transpose of an m-by-n matrix with complex entries is the n-by-m matrix obtained from by taking the transpose and then taking the complex conjugate of each entry the complex conjugate of being for real numbers and It is often denoted as or.
In mathematics particularly in linear algebra matrix multiplication is a binary operation that produces a matrix from two matrices. That is any number times 1 is equal to itself. I b 0 do i 1 n b ii 1 end do end function identity.
Next perform vari-ous linear operations on the left-side matrix to reduce it to an identity matrix. The transpose of the sum of two matrices is equivalent to the sum of their transposes. Then we can write ABCT ABCT.
The transpose of the product of two matrices is equivalent to the product of their transposes. ANOTHER way is to check and see if matrix R times the transpose of matrix R equals the Identity matrix of R. Because AxA transpose A transposexA thats why we cant say that A x A-transpose is invertible.
Given a matrix and a matrix operation identify the contents of the resulting matrix eg SSCP Covariance Correlation. When for what kind of matrix does the transpose of a matrix equal the original matrix. There are two cases i j and i j.
Note also the equivalent definition of a real orthogonal.
Identity Matrix Intro To Identity Matrices Article Khan Academy

What Is An Identity Matrix Studypug

Introduction To Matrices Boundless Algebra
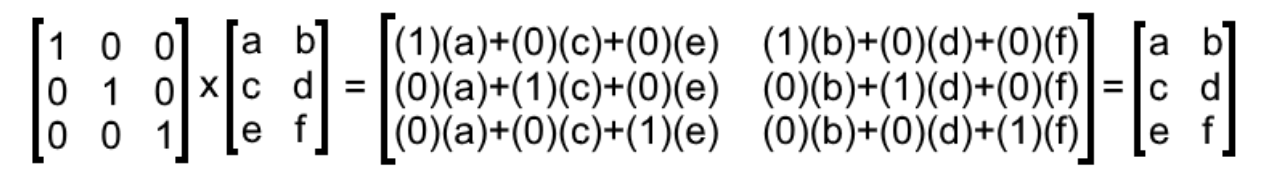
What Is An Identity Matrix Studypug

The Identity Matrix And Its Properties Mathbootcamps
Matrix Matrix Multiplication Ml Wiki
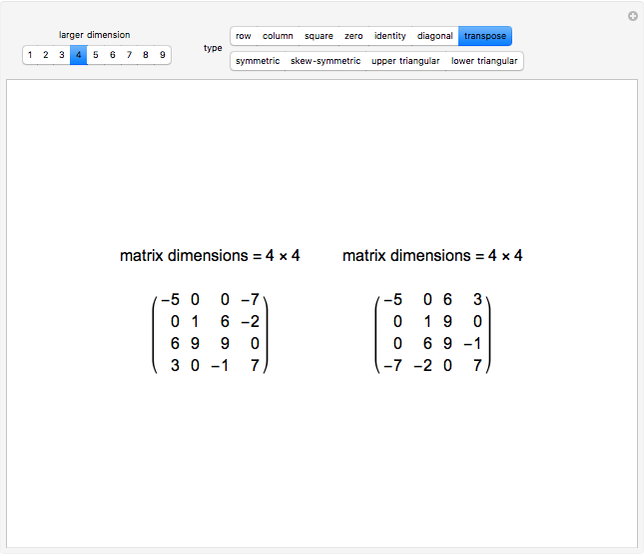
Some Special Types Of Matrices Wolfram Demonstrations Project
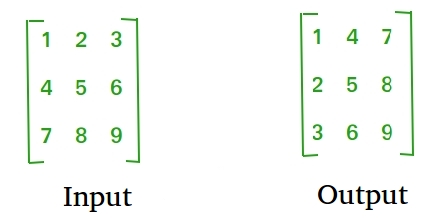
Python Program To Find Transpose Of A Matrix Geeksforgeeks

Divide And Conquer Set 5 Strassen S Matrix Multiplication Tutorialspoint Dev

The Identity Matrix And Its Properties Mathbootcamps
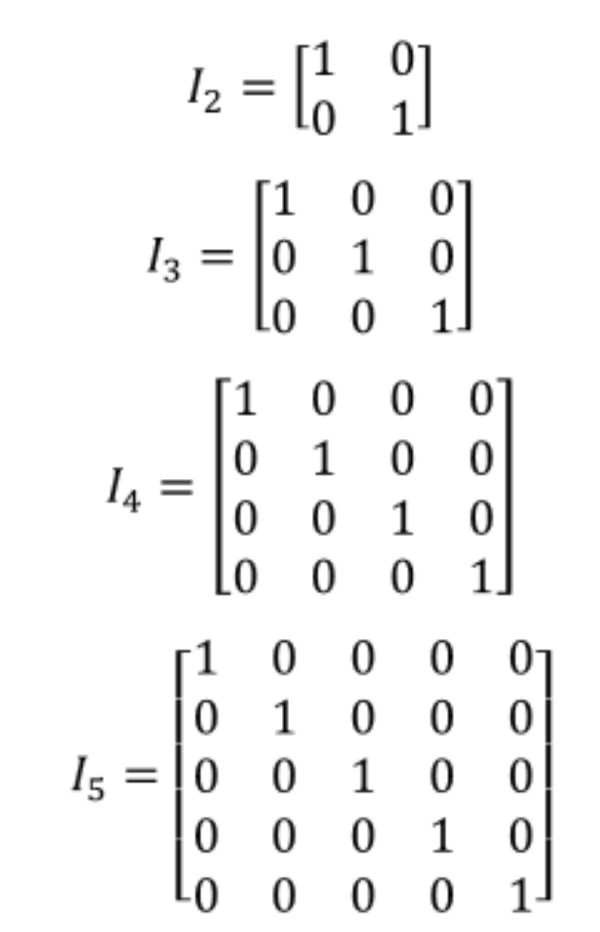
What Is An Identity Matrix Studypug

The Identity Matrix And Its Properties Mathbootcamps
Matrix Definition Of A Matrix Examples Of A Matrix Elements
Multiplying Matrices Article Matrices Khan Academy
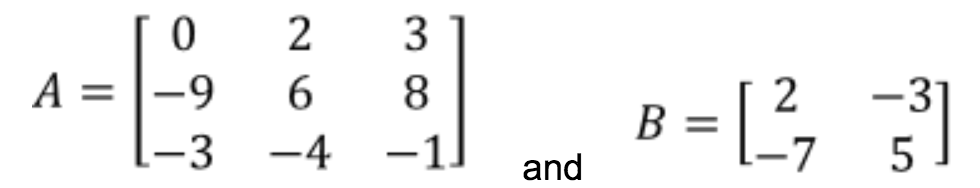
What Is An Identity Matrix Studypug