Is Scalar Triple Product Associative

14 Jul, 2021

6 where Einstein summation has been used to sum over repeated indices. A b c.

Vector Triple Product Expansion Very Optional Video Khan Academy

Triple product In vector algebra a branch of mathematics the triple product is a product of three 3- dimensional vectors usually Euclidean vectors.

Is scalar triple product associative. To begin with we recommend you first master the cross product. The basic point is that a difference of associative bilinear products will still be bilinear but need not be associative at all. 1Ifoverrightarrowalpha overrightarrowbeta overrightarrowgamma bethreevectorsthenleft overrightarrowalpha.

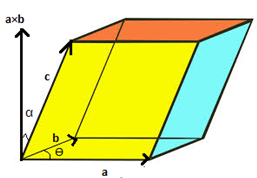
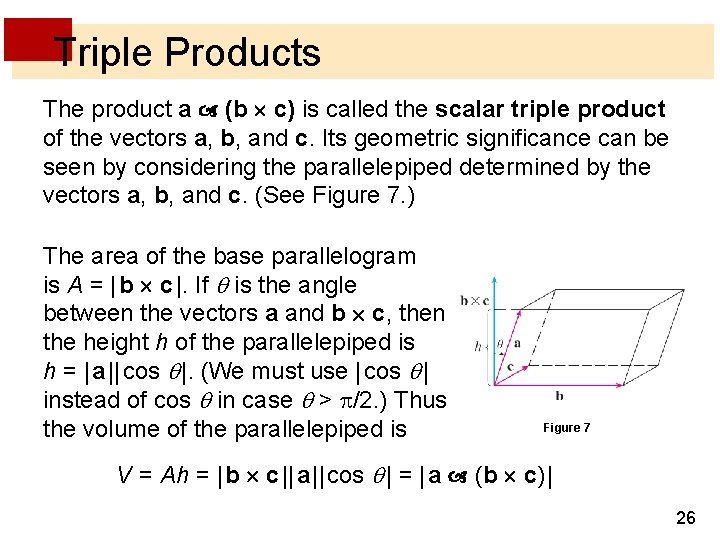
B c is a scalar multiplied by the vector c. Like dot product was a scalar product this is also a scalar product but there will be three vector quantities a b and c. The scalar triple product is obviously very useful if you have a lot of parallelepipeds lying around and want to know their volume.

Cz in the Cartesian coordinate system can be calculated using the following formula. But if you dont happen to find yourself pining to know the volume of a parallelepiped you may wonder whats the use of the scalar triple product. If α βand γbe three vectors then the product α X β.

Scalar Triple Product. Scalar triple product of vectors is equal to the determinant of the matrix formed from these vectors. So as the name suggests triple means there are three quantities.

The scalar triple product can also be written in terms of the permutation symbol as. As the exterior product is associative brackets are not needed as it does not matter which of a b or b c is calculated first though the order of the vectors in the product does matter. The triple product has two different operations a vector product and a scalar product.

If you have only enough available brain cells to master either the cross product or the scalar triple product wed recommend focusing on the cross. By the same argument u v w is coplanar with v and w. If the triple scalar product is 0 then the vectors must lie in the same plane meaning they are coplanar.

To see why this should be so we note that u v w is perpendicular to u v which is normal to a plane determined by u and v. Properties of Triple Scalar Product. Yes the value of the scalar triple product of vectors can be positive negative or zero.

Hazard The vector triple product is not associative ie. Note α β γ is a scalar quantity. The scalar triple product is defined.

What would be the effect of changing the parentheses. Given vectors a b and c the product is a trivector with magnitude equal to the scalar triple product and is the Hodge dual of the vector triple product. This volume is independent of how the triple product is formed from and except that.

It is denoted by α β γ. Vector a vector b vector c and it is a scalar product. U v w u v w.

The scalar triple product is a pseudoscalar ie it reverses sign under inversion. Is a scalar triple product associative. γis called triple scalar product or box product of.

Ab c ca b bc a easily derived by working in components. Now is the vector area of the parallelogram defined by and. The scalar product of two vectors is a scalar.

311 Properties of scalar triple product I It is obvious that ab c b ca I Cyclic permutations of a b and c leaves the triple scalar product unaltered. Abc cab bca acb cba bac. I Non-cyclic permutations change sign.

Can a scalar triple product be negative. Az b bx. Scalar triple product of vectors a ax.

So u v w is coplanar with u and v. Still its instructive to get an explicit expression for the associator of the cross product. So is the scalar area of this parallelogram times the component of in the direction of its normal.

It follows that is the volume of the parallelepiped defined by vectors and see Fig. The scalar triple product formula represents the parallelepiped volume whose three coterminous edges represent the three vectors a b and c. The cross product of two vectors a and b is defined only in three-dimensional space and is denoted by a b.

In physics and applied mathematics the wedge notation a b is often used in conjunction with the name vector product although in pure mathematics such notation is usually reserved for just the exterior product an abstraction of the vector product to n dimensions. The cross product defines a Lie algebra structure on thus it is anti-commutative and for triple products the Lie identity holds. B c is the dot product of the vectors a and b c.

Additional identities involving the. Bz and c cx. The name triple product is used for two different products the scalar-valued scalar triple product and less often the vector-valued vector triple product.

No it is not associative.

12 Vectors And The Geometry Of Space Copyright