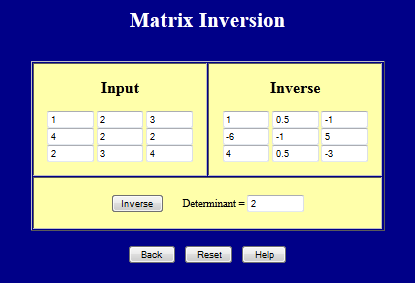
Invertible Matrix And Inner Product
1 Real inner products Let v v 1v n and w w 1w n 2Rn. Introduction An indefinite inner product in is a conjugate symmetric sesquilinear from together with the regularity condition that.
Solved A Let Aernxn Be An Invertible Matrix Prove That Chegg Com
De ne the length or norm of vby the formula kvk p hvvi q v2 1 v2n.
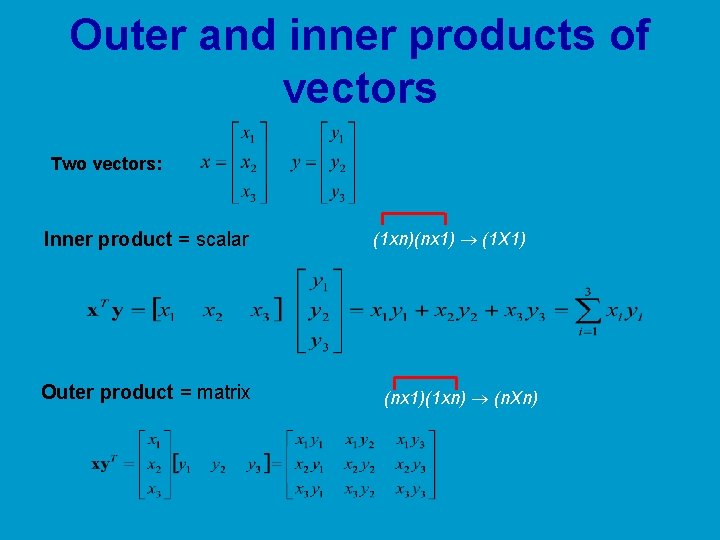
Invertible matrix and inner product. For finite-dimensional vector spaces V and W over the same field F let V W indicate that there is a linear transformation TV W which is an isomorphism. Let N be an invertible hermitian matrix of order n. We call u and v orthogonal if u v 0 where u v C n.
Then jju vjj p 2. Prove that A is invertible and the inverse matrix is given by the formula A-1I-amathbfumathbfvtrans where afrac11mathbfvtransmathbfu. Hvwi v 1w 1 v nw n.
Note that we can de ne hvwifor the vector space kn where kis any eld but kvkonly makes sense for k R. The two matrices must have the same dimensionsame number of rows and columnsbut are not restricted. Conversely some inner product yields a positive definite matrix.
It is often denoted A B F displaystyle langle mathbf Amathbf B rangle _mathrm F. Mv Ma 1v 1 a nv n 2 6 6 6 4 a 1 a 2. If A is a real symmetric positive definite matrix then it defines an inner product on Rn.
Jju vjjis the square root of u vu v uu 2uvvv 2. Inner Products Generated by Matrices Let be vectors in Rn expressed as n 1 matrices and let A be an invertible n n matrix. If u v is the Euclidean inner product on Rn then the formula u v Au Av 1 1 2 2and.
An indefinite inner product in C n is defined by the equation x y x N y where x y C n. Express the invertible matrix A below as a product of elementary matrices. 164 CHAPTER 6 Inner Product Spaces 6A Inner Products and Norms Inner Products x Hx x L 1 2 The length of this vectorp xis x 1 2Cx 2 2.
We have the following properties for the inner product. A 0b 02a 0b 13a. If hxyi h yxiin some inner product space then xis orthogonal to y.
Is an inner product on V if and only if. A 1 2 - 1 0 1 3 0 0 2 Problem 9. Such a matrix N is called a weight.
A space with an indefinite inner product is called an indefinite inner product space IIPS. If V P 2R then the following is an inner product on V. Let uand vbe any two orthonormal vectors in an inner product space.
You can conjugate it but it doesnt make sense to ask for its adjoint unless you multiply it by some operator and it certainly doesnt make sense to ask for its inverse. N n u v u v u v u v 20081217 Elementary Linear Algebra 15 defines an inner product. We de ne the inner product or dot product or scalar product of v and w by the following formula.
Similarly the product A T A is a symmetric matrix. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. Begingroup An inner product does not have an inverse.
Fn is the usual coordinate map given by. If p i j is the entry of the product it is obtained from rows i and j in A. The entry p j i is also obtained from these rows thus p i j p j i and the product matrix p i j is symmetric.
Inner products on V. It is called the inner product on Rn generated by A. We know hxyi hyxiby the symmetric property of inner products so the hypothesis forces hxyi 0.
But the columns of A T are the rows of A so the entry corresponds to the inner product of two rows of A. Mx AMy where Ais a self-adjoint matrix with positive eigenvalues 5 where M. The expression langle xyrangle is just a complex number.
Indefinite matrix product Indefinite inner product space Range symmetric matrix EP matrix AMS Mathematics Subject Classification 2010. The operation is a component-wise inner product of two matrices as though they are vectors. In mathematics the Frobenius inner product is a binary operation that takes two matrices and returns a number.
To motivate the concept of inner prod-uct think of vectors in R2and R3as arrows with initial point at the origin. A n 3 7 7 7 5 Example. Murray Jan 5 at 156.
Stack Exchange network consists of 176 QA communities including Stack Overflow the largest most trusted online community for developers to learn share their knowledge and build their careers.

Problem 8 Below I V 1 Is Inner Product In Chegg Com
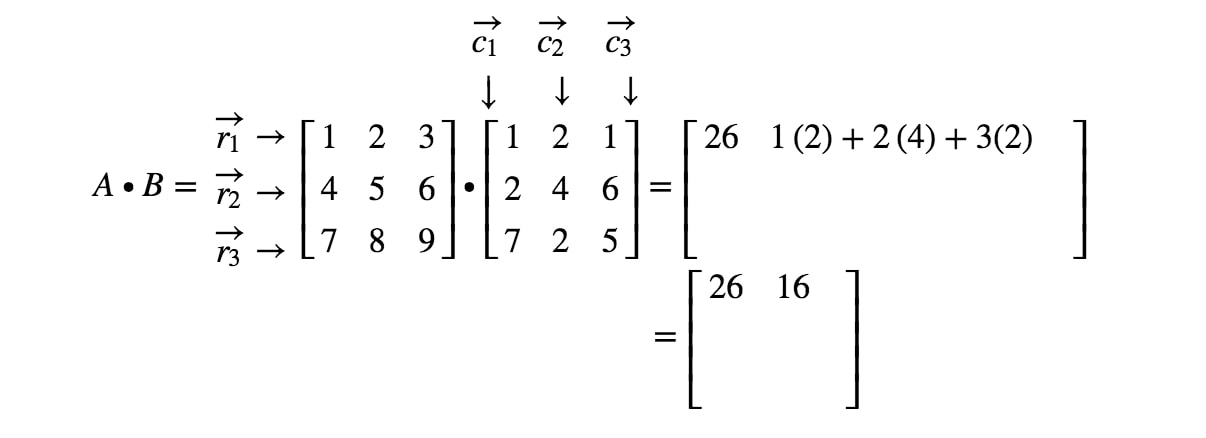
How To Multiply Two Matrices Together Studypug

Let A E Mn C Be An Invertible Matrix And Define A Chegg Com

Elementary Linear Algebra Anton Rorres 9th Edition Ppt Download

Let A Be An Invertible Nxn Matrix There Is An Inn Chegg Com

Linear Algebra Matrices And Why They Matter To
4 Let V Be The Vector Space Of All N N Matrices Chegg Com

A Matrix Inner Product Defined On R N Is Generated By Chegg Com

Solved Linear Algebra Proof Suppose That V Is An Inner Pr Chegg Com

If The Inner Product Of Two Matrices Is Zero What Does That Mean

Linear Algebra Lecture 25 The Invertible Matrix Theorem Youtube

Showing That A Transpose X A Is Invertible Video Khan Academy
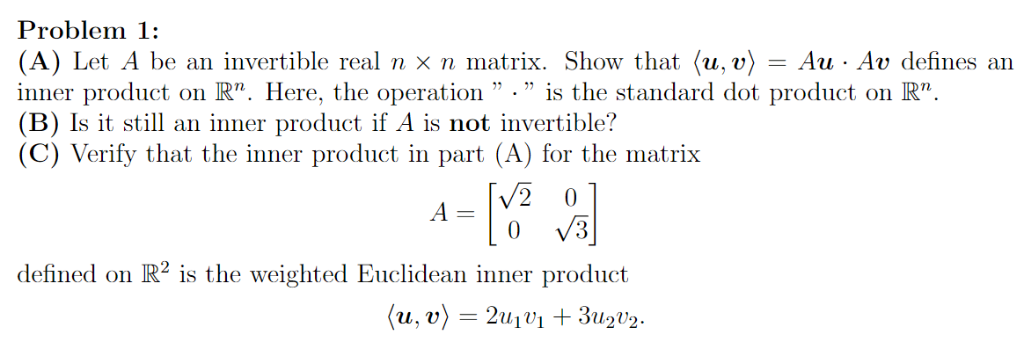
Problem 1 A Let A Be An Invertible Real N X N Chegg Com
Showing That A Transpose X A Is Invertible Video Khan Academy

If The Inner Product Of Two Matrices Is Zero What Does That Mean