Winograd Matrix Multiplication Algorithm
In 2005 together with Kleinberg and Szegedy 7 they obtained several novel matrix multiplication algorithms using the new framework however they were not able to beat 2376. De nition 5 rank.

Pdf Multiplying Matrices Faster Than Coppersmith Winograd Semantic Scholar
However the constant is so large that this algorithm is in fact slower in practice than naive matrix multiplication for small n.

Winograd matrix multiplication algorithm. For matrix multiplication U V W Fn n and we write this bilinear map as hnnni. Coecient of Strassen-Winograds algorithm was believed to be optimal for matrix multiplication algorithms with 2 2 base case due to a lower bound of Probert 1976. In fact both Coppersmith and Winograd.
Take Matrices M1 M2 M3 as an input of nn. Journal of Symbolic Computation 1990. Verify if M1 M2 a - M3 a 0 or not.
If it is zero or false then matrix multiplication is correct otherwise not. Strassen discovered that the classic recursive MM algorithm of complexity On3 can be reorganized in such a way. An On2 log n algorithm would fit the bill.
Choose matrix an1 randomly to which component will be 0 or 1. Spencer 1942 to get an algorithm with running time ˇ On2376. For a long time this latter algorithm had been the state of the art.
Thus these algorithms provide better performance when used together with. Many researchers believe that the true value of is 2. You can get a back-of-the-envelope feeling for a lower bound on the exponent of Coppersmith-Winograd based on the fact that people dont use it even for n on the order of 10000.
Used a thm on dense sets of integers containing no three terms in arithmetic progression R. Col for the Strassen-Winograd matrix multiplication algorithm. An interesting new group theoretic approach.
Setting the expressions equal and solving for C gives. The ikj single core algorithm implemented in Python needs. The Cook-Toom algorithm based on Lagrange Interpolation and the Winograd Algorithm based on the Chinese remainder theorem C H D x b a d c d c d f e s 1 1 0 1 1 0 0 0 0 0 0 0 0 1 1 1 0 1.
Adaptive Winograds Matrix Multiply 3 that have asymptotic complexity less than ON3 and we use the term classic or con-ventional algorithms for those that have complexity ON3. Applying their technique recursively for the tensor square of their identity they obtain an even faster matrix multiplication algorithm with running time On2376. Then the rank of R is the smallest r2N such that uv Xr i f iug ivw i 4 For w i 2W and f and gare F-linear forms a linear transformation from a.
Naive matrix multiplication requires 2n3 On2 flops and Coppersmith-Winograd requires Cn2376 On2. Fast and stable matrix multiplication p744. Rently fastest matrix multiplication algorithm with a complexity of On238 was obtained by Coppersmith and Winograd 1990.
Time python ikjMultiplicationpy -i 2000in 2000-nonparallelout real 36m0699s user 35m53463s sys 0m2356s. Fast short-length convolution algorithms. Calculate M2 a M3 a and then M1 M2 a for computing the expression M1 M2 a - M3 a.
Let be a F-bilinear map. There exist asymptotically faster matrix multiplication algorithms eg the Strassen algorithm or the Coppersmith-Winograd algorithm which have a slightly faster rate than O n 3. Persmith and Winograd were able to extract a fast matrix multiplication algorithm whose running time is On2388.
Similarly the Coppersmith-Winograd algorithm which has the lowest asymptotic complexity of all known matrix multiplication algorithms has an exponent of. We focus on the setting in which any given player knows only one row or one block of rows of both input matrices and after the computation only has ac-cess to the corresponding row or block of rows of the resulting product matrix. For given matrices A and B the Strassen and Winograd algorithms for matrix multiplication being categorized in the divide-and-conquer algorithms can reduce the number of additions and multiplications compared to the normal matrix multiplication particularly for large-sized matrices.
Surprisingly we obtain a faster matrix multiplication algorithm with the same base case size and asymptotic complexity as Strassen-. Don Coppersmith Shmuel Winograd Matrix multiplication via arithmetic progressions. Parallelized Strassen and Winograd Algorithms.
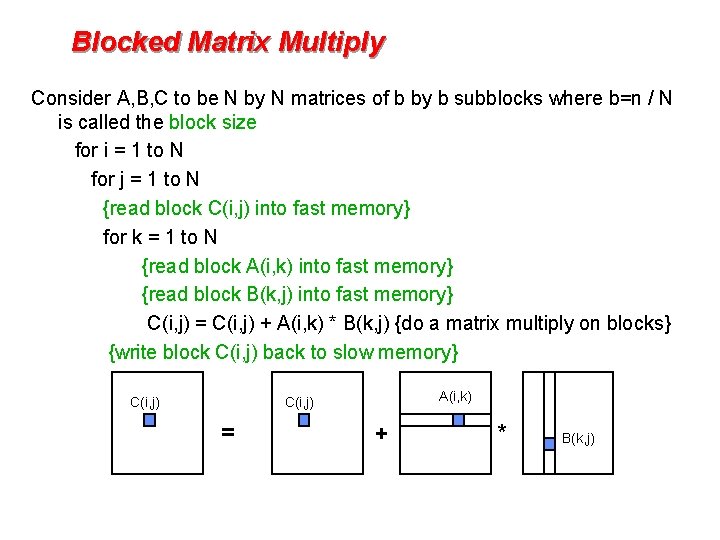
More information on the fascinat-ing subject of matrix multiplication algorithms and its history can be found in Pan 1985 and Burgisser et al. The most simple way to parallelize the ikj algorith is to use the multiprocessing module and compute every line of the result matrix.

Table 1 From Fast Matrix Multiplication Limitations Of The Coppersmith Winograd Method Semantic Scholar

Matrix Multiplication Coppersmith Winograd And Beyond Youtube

Matrix Multiplication Intro To Algorithms Youtube

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
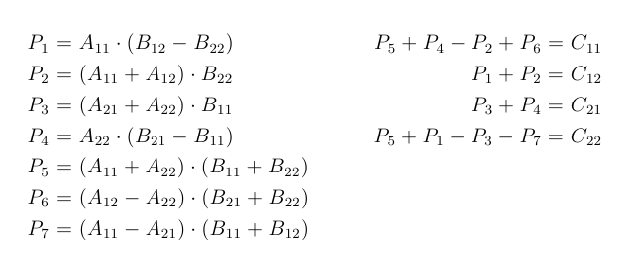
Strassen Matrix Multiplication C The Startup

Fast Matrix Multiplication And Graph Algorithms Uri Zwick

Figure 5 From Auto Blocking Matrix Multiplication Or Tracking Blas3 Performance From Source Code Semantic Scholar
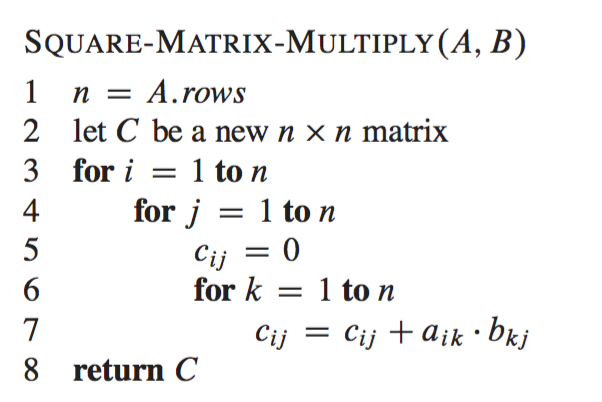
Matrix Multiplication Using The Divide And Conquer Paradigm

Complexity Of Various Algorithms For Matrices Multiplication 9 10 11 Download Table

Matrix Multiplication Algorithm Wikiwand

Matrix Multiplication Algorithm Wikiwand

Matrix Multiplication Algorithm Wikiwand

Matrix Multiplication Verifying Strong Uniquely Solvable Puzzles Springerlink
Cs 140 Matrix Multiplication Matrix Multiplication I Parallel

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Communication Costs Of Strassen S Matrix Multiplication February 2014 Communications Of The Acm

What Is Coppersmith Winograd S Algorithm To Multiply Matrixes And How It Gives O N 2 37 Time Complexity Quora

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Figure 1 From Recursive Array Layouts And Fast Matrix Multiplication Semantic Scholar