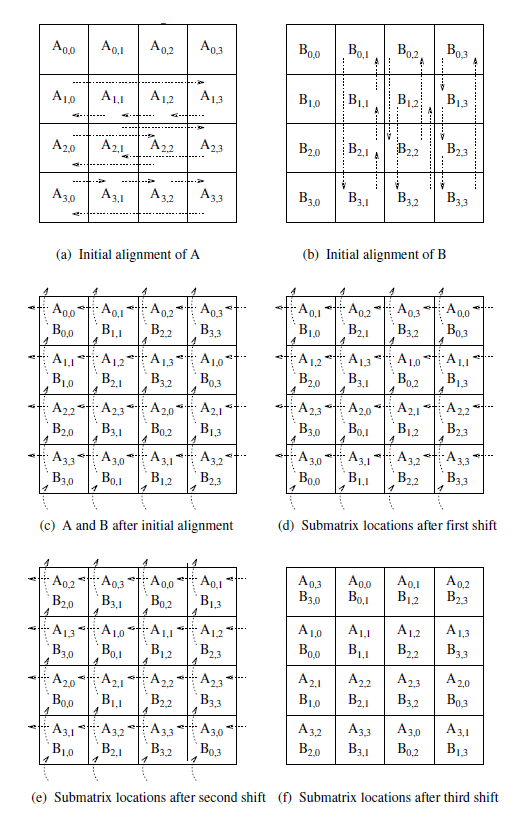
What Is The Time Complexity Of Matrix Multiplication Algorithm
Strassens Matrix multiplication can be performed only on square matrices where n is a power of 2. 5 6 1 7 Enter the 4 element of second matrix.

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
Provides an upper bound.

What is the time complexity of matrix multiplication algorithm. As before if we have n matrices to multiply it will take O n time to generate each of the O n2 costs and entries in the best matrix for an overall complexity of O n3 time at a cost of O n2 space. MATHPOWER M n if n 1 then return M else P MATHPOWER M floorn2 if n mod 2 0 then return P P else return P P M Share. Minimum number of multiplications is 30 The time complexity of the above naive recursive approach is exponential.
For k i to j-1 9. Review Strassens sequential algorithm for matrix multiplication which requires Onlog 2 7 On281 operations. It should be noted that the above function computes the same subproblems again and again.
Algorithm of Matrix Chain Multiplication MATRIX-CHAIN-ORDER p 1. Mij 8. Ignore minor details such as the house keeping aspects of the algorithm.
In general multipling two matrices of size N X N takes N3 operations. The time complexity is ON 28074. Recently I have learned about both the Strassen algorithm and the CoppersmithWinograd algorithm independently according to the material Ive used the latter is the asymptotically fastest known matrix multiplication algorithm until 2010.
Browse other questions tagged algorithms time-complexity matrices or ask your own question. 25 minutes Coding time. Note that the operator denotes ordinary matrix multiplication.
Addition of two matrices takes O N 2 time. The best known algorithm has complexity approximately O n23728639. Do m i i 0 4.
For l 2 to n l is the chain length 5. See the following recursion tree for a matrix chain of size 4. The fastest known matrix multiplication algorithm is Coppersmith-Winograd algorithm with a complexity of O n 23737.
The algorithm is amenable to parallelizable4 A variant of Strassens sequential algorithm was developed by Coppersmith and Winograd they achieved a run time of On23753. A lower bound is certainly O n2. Do q m i k m k 1 j p i-1 p k p j 10.
The constants used in Strassens method are high and most of the time the Naive method works better. In the above method we do 8 multiplications for matrices of size N2 x N2 and 4 additions. Strassens Matrix Multiplication Algorithm In this context using Strassens Matrix multiplication algorithm the time consumption can be improved a little bit.
In practice it is easier and faster to use parallel algorithms for matrix multiplication. Operations addition multiplication etc. Matrix Multiplication is one of the most fundamental operation in Machine Learning and optimizing it is the key to several optimizations.
Enter the 4 elements of first matrix. For i 1 to n 3. Time complexity O n log 72 O n28074 The O n 28074 is slightly lesser than O n 3 but this method is usually not preferred for the practical purposes.
6 2 8 7 The first matrix is 5 6 1 7 The second matrix is 6 2 8 7 After multiplication 78 52 62 51 Complexity. The naive algorithm has complexity O mjn for multiplying an m x j matrix by a j x n matrix or O n3 for square n x n matrices. Unless the matrix is huge these algorithms do not result in a vast difference in computation time.
Matrix Multiplication Consider nn matrix multiplication with n3 processors Each c ij k1n a ik b kj can be computed on the CREW PRAM in parallel using n processors in Olog n time On the EREW PRAM exclusive reads of a ij and b ij values can be satisfied by making n copies of a and b which takes Olog n time with n processors broadcast tree. Focus on the worst-case time complexity of an algorithm. However it is unknown what the underlying complexity actually is.
Hence the algorithm takes O n3 time to execute. Do for i 1 to n-l 1 6. Do j i l -1 7.
More difficult to determine the average case time complexity of an algorithm average. So the time complexity can be written as T N 8T N2 O N 2 From Masters Theorem time complexity of above method is O N 3 which is unfortunately same as the above naive method. As It can multiply two n n matrices in 0 n2375477 time.

Communication Costs Of Strassen S Matrix Multiplication February 2014 Communications Of The Acm
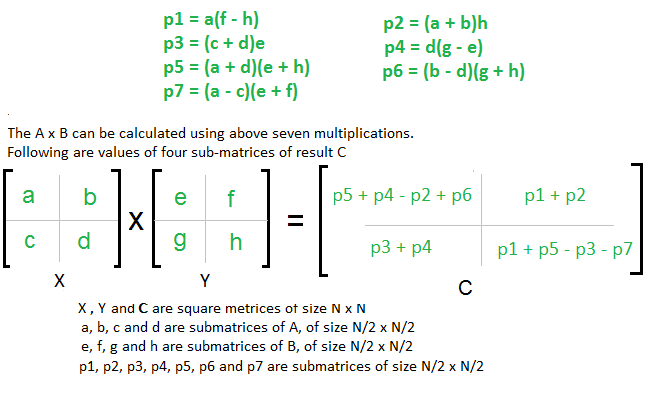
Easy Way To Remember Strassen S Matrix Equation Geeksforgeeks

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Matrix Chain Multiplication Explained Kilichbek Haydarov

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Systolic Arrays Algorithm For Matrix Multiplication Mathematics Stack Exchange

2 9 Strassens Matrix Multiplication Youtube
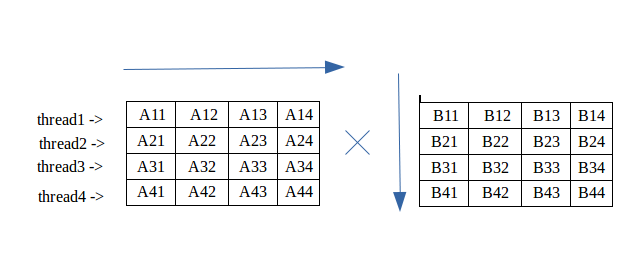
Multiplication Of Matrix Using Threads Geeksforgeeks
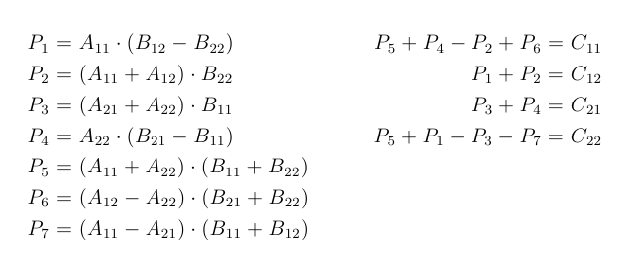
Strassen Matrix Multiplication C The Startup
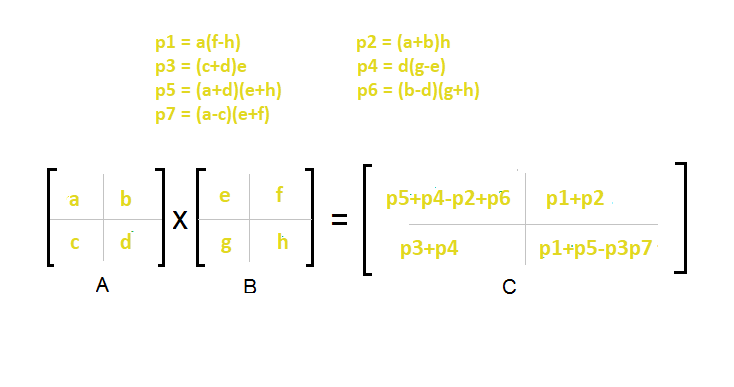
Strassen S Matrix Multiplication Algorithm
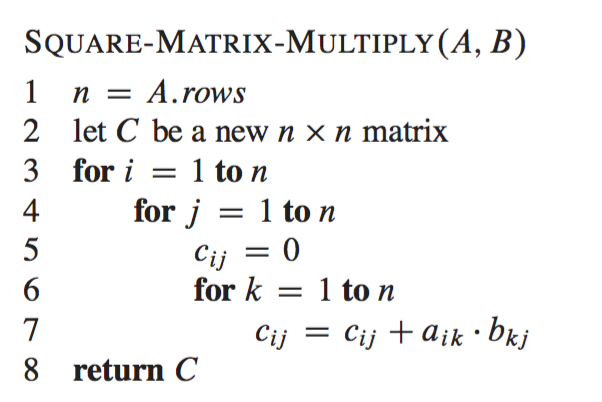
Matrix Multiplication Using The Divide And Conquer Paradigm
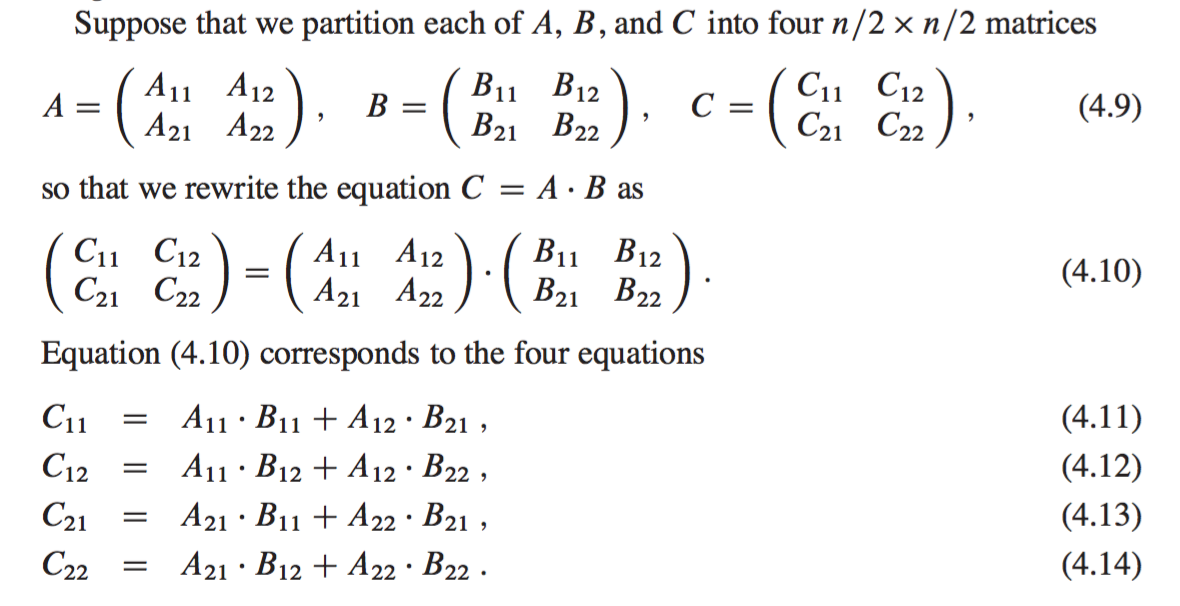
Matrix Multiplication Using The Divide And Conquer Paradigm

Strassen S Matrix Multiplication Algorithm When N Is Not A Power Of 2 Computer Science Stack Exchange

Time Complexity Of Strassen S Matrix Multiplication In Daa Design And Analysis Of Algorithms Youtube

Time Complexity Of Some Matrix Multiplication Mathematics Stack Exchange

Strassen S Matrix Multiplication Divide And Conquer Geeksforgeeks Youtube

Time Complexity Of Clrs Optimal Parenthesis Algorithm Mathematics Stack Exchange
Cannon S Algorithm For Distributed Matrix Multiplication

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov