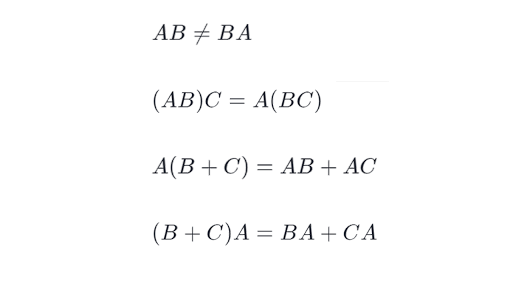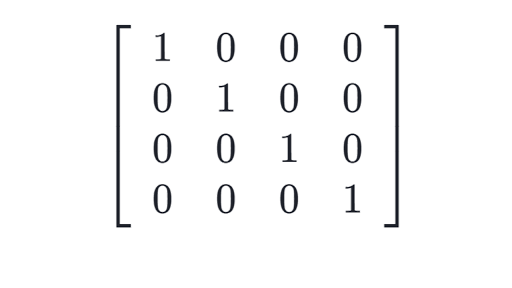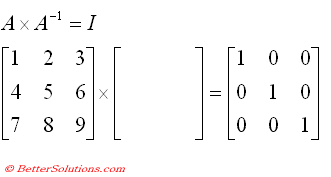Rules Of Multiplying Identity Matrices
We define A I where I is the identity matrix. In other words if all the main diagonal of a square matrix are 1s and rest all os it is called an identity matrix.
What Is An Identity Matrix Studypug
Multiplying a matrix by the identity matrix I thats the capital letter eye doesnt change anything just like multiplying a number by 1 doesnt change anything.
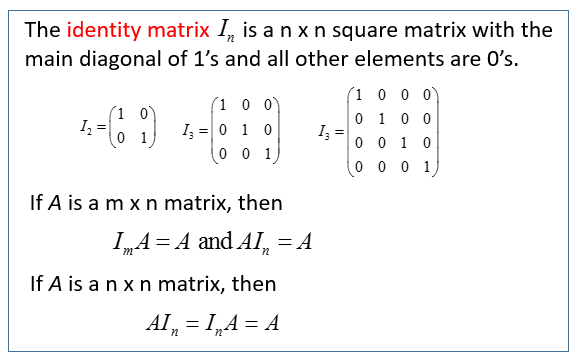
Rules of multiplying identity matrices. The last special case of matrix multiplication involves the identity matrix I. Matrix multiplication not commutative In general AB BA. I think this only work when the matrix A is square matrix.
If any matrix is multiplied with the identity matrix the result will be given matrix. Eg A is 2 x 3 matrix B is 3 x 5 matrix eg A is 2 x 3 matrix B is 3 x 2 matrix. The identity matrix operates as the number 1 does in scalar algebra.
To make the statement AIA to be true the identity matrix need to be 2x2 matrix. If they arent equal then matrix multiplication is undefined. We can take powers of matrices but only if theyre square.
Note however that a scalar multiplied by an identify matrix becomes a. If A is not square then A A doesnt work for matrix multiplication. Hence aI a IX X etc.
If A is a square matrix then A A is well-defined. Problems with hoping AB and BA are equal. Here the 2 x 2 and 3 x 3 identity matrix is given below.
BA may not be well-defined. Even if AB and BA are both defined and of the same size they still may not be equal. But to make the statement IAA to be true the identity matrix in this case need to be a 3x3 matrix.
If they are equal we can multiply the 2 matrices together. Even if AB and BA are both defined BA may not be the same size. That is any vector or matrix multiplied by an identity matrix is simply the original vector or matrix.
For example we have a 3x2 matrix. The usual rules for exponents namely P and AP still apply. The resulting matrix will have a dimension equal to the number of rows of the 1st matrix and the number of columns of the 2nd matrix.
This property of leaving things unchanged by multiplication is why I and 1 are each called the multiplicative identity the first for matrix multiplication the latter for numerical multiplication. The elements of the given matrix remain unchanged.
The Identity Matrix And Its Properties Mathbootcamps
Question Video Multiplication Of Two Matrices Involving The Identity Matrix Nagwa
Inverse Of A Square Matrix Online Presentation
What Is An Identity Matrix Studypug
Identity Matrix Andymath Com
Inverse Identity Matrices Ppt Video Online Download
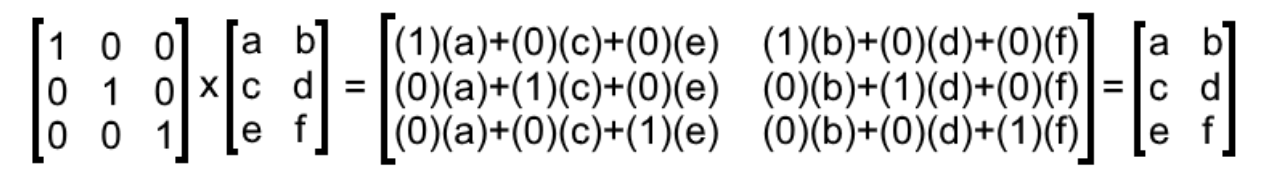
What Is An Identity Matrix Studypug
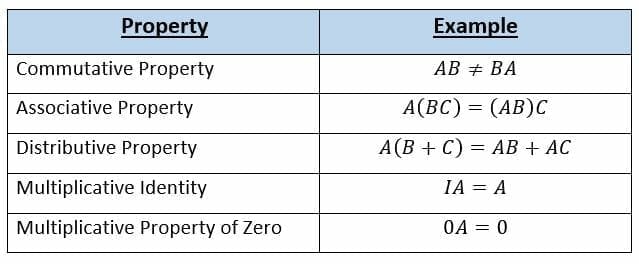
Properties Of Matrix Multiplication Article Khan Academy
Matrices
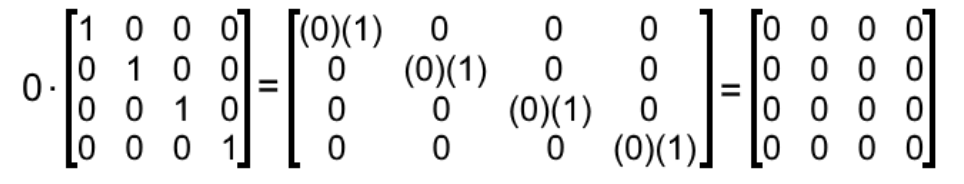
What Is An Identity Matrix Studypug
Lecture 4 Rules Of Matricies Ppt Video Online Download
The Identity Matrix And Its Properties Mathbootcamps
Rules Of Matrix Arithmetic Ppt Video Online Download
Ldapwiki Identity Matrix
Identity Matrix Intro To Identity Matrices Article Khan Academy
Matrix Multiplication Explanation Examples
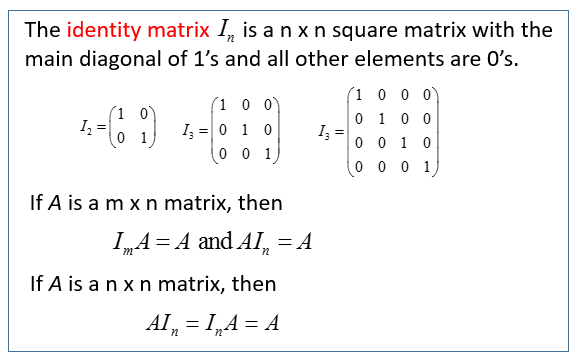
Zero Identity And Inverse Matrices Solutions Examples Videos Worksheets Games Activities
What Is An Identity Matrix Studypug
Excel Matrix Functions
