Matrix Multiplication Complexity Lower Bound
The bounds are obtained by. For a tensor T let RT denote its border rank.

Lower And Upper Bound Theory Geeksforgeeks
Proceedings 2001 IEEE International Conference on Cluster Computing 358-367.
Matrix multiplication complexity lower bound. 9 for matrix multiplication we present conditional group-theoretic lower bounds for the complexity of matrix multiplication. Our bounds are betterthan the previous lower bound due to Lickteig in 1985 of3n22n21for alln3The bounds are obtained by finding new equations that bilinear maps of small border rankmust satisfy i. This bound even holds for the multiplicative complexity.
Unless the matrix is huge these algorithms do not result in a vast difference in computation time. Holtz Chair Via novel path-routing techniques we prove a lower bound on the IO-complexity of all recursive matrix multiplication algorithms computed in serial or in parallel and show that it is tight for all square and near-square matrix multiplication. Optimal for matrix multiplication algorithms with 2 2 base case due to a lower bound of Probert 1976.
Lower bounds for matrix product. However this bound does not give any good results for n. Asymptotically the best lower bound for nn-matrix multiplication over arbitrary fields is Rnnn 5 2 n 2 3n see.
For smaller formats we have 1 Rℓmnℓmmnℓmn3 for nℓ2 see. 40th Annual Symposium on Foundations of Computer Science Cat. Using techniques from algebraic geometry and representation theory we show the border rank is at least 2n2 n.
Exponent of Rectangular Matrix Multiplication. 1 Abstract An IO-Complexity Lower Bound for All Recursive Matrix Multiplication Algorithms by Path-Routing by Jacob N. Using techniques from algebraic geometry andrepresentation theory we show the border rank is at least 2n2n.
Our bounds are better than the previous lower bound due to Lickteig in 1985 of 3 2 n2 n 2 1 for all n 3. Standard measure of its complexity. To lower bound the value of a tensor in designing ma-trix multiplication algorithms.
Surprisingly we obtain a faster matrix multiplication algorithm with the same base case size and asymptotic complexity as Strassen-Winograds algorithm but with the coecient reduced from 6 to 5. The laser method also has applications beyond bounding itself including to other problems in arithmetic complexity like comput-ing the asymptotic subrank of tensors Alm19 and to. Up to 10 cash back We prove a lower bound of km mn km n 3 for the multiplicative complexity of the multiplication of k times m Lower bounds for the multiplicative complexity of matrix multiplication SpringerLink.
Using Bläsers lower bounds for the rank of associative. In modern literature this result is virtually unknown and I am not aware of any other lower bound on matrix multiplication beyond the Ω n 2 lower bounds of Bshouty and Shpilka and the Ω n 2 log n lower bound of Raz. More general we show that for any finite dimensional semisimple algebra A with unity the multiplicative complexity of the multiplication in A is bounded from below by 2 dimA Gamma 3 n1 Delta Delta Delta n t if the decomposition of A A1 Theta Delta Delta Delta Theta A t into simple algebras A D contains only noncommutative factors that is the division algebra D is noncommutative or n 2.
Computational complexity circuit lower bounds The problem with m n appears as the bottleneck in many applications. Scott Doctor of Philosophy in Mathematics University of California Berkeley Professor Olga V. These bounds depend on the complexity of multiplication in group algebras.
The fastest known matrix multiplication algorithm is Coppersmith-Winograd algorithm with a complexity of On 23737. There is a lower bound for multiplication of Ω n log n conditional on a conjecture in network coding. E new equations for secant varieties of triple Segre.
A 52nsup 2-lower bound for the rank of nn-matrix multiplication over arbitrary fields. Let Muvwe C uvCvwCwu denote the matrix multiplication tensor and write Mne Mnnne and let det 3 C 93 denote the determinant polynomial considered as a tensor. The border rank of the matrix multiplication operator for n n matrices is a stan-dard measure of its complexity.
There is also an algorithm matching this bound. Up to 10 cash back Inspired by the recent group-theoretic approach by Cohn and Umans 10 and the algorithms by Cohn et al. NEW LOWER BOUNDS FOR MATRIX MULTIPLICATION AND det 3 AUSTIN CONNER ALICIA HARPER AND J.
Solvay Strassen algorithm achieves a complexity of On 2807 by reducing the number of multiplications required for each 2x2 sub-matrix from 8 to 7.
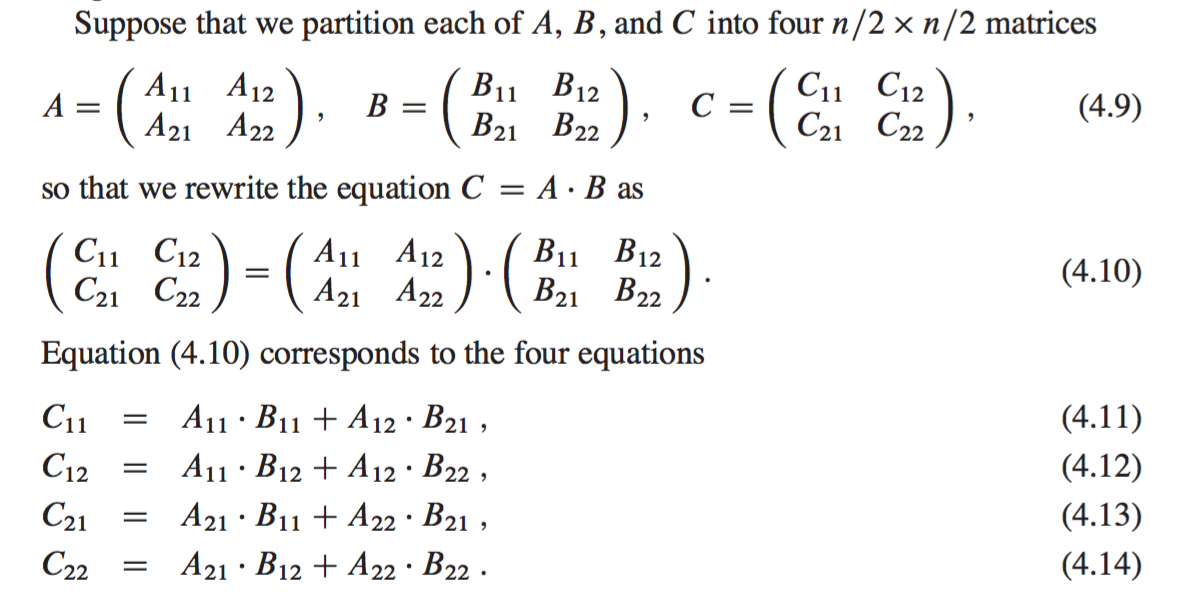
Matrix Multiplication Using The Divide And Conquer Paradigm

Daa Lower Bound Theory Javatpoint

Numerical Algorithms Matrix Multiplication Ppt Download

Numerical Algorithms Matrix Multiplication Ppt Download
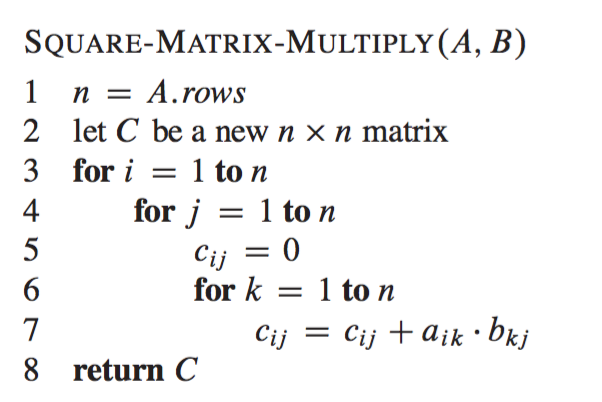
Matrix Multiplication Using The Divide And Conquer Paradigm

Lower And Upper Bound Theory Geeksforgeeks
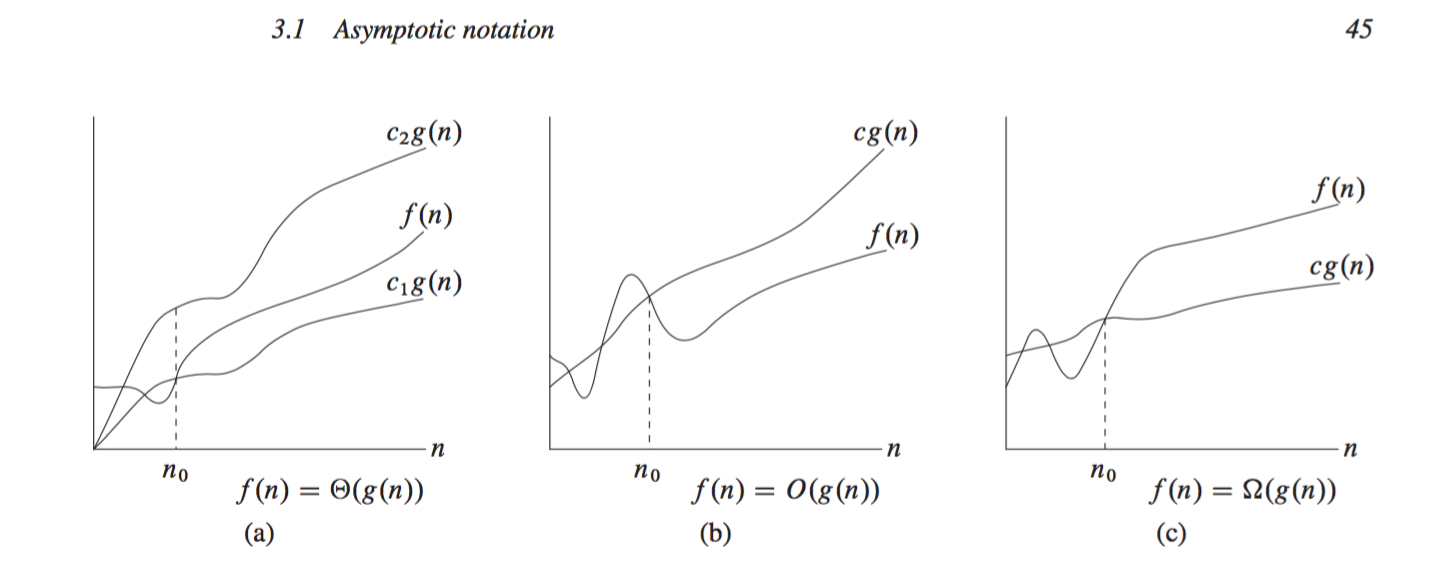
Matrix Multiplication Using The Divide And Conquer Paradigm

Pdf A Lower Bound For Matrix Multiplication

Matrix Multiplication Algorithm Wikiwand

Numerical Algorithms Matrix Multiplication Ppt Download

Matrix Multiplication With 1 Mapreduce Step Geeksforgeeks

Communication Costs Of Strassen S Matrix Multiplication February 2014 Communications Of The Acm

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
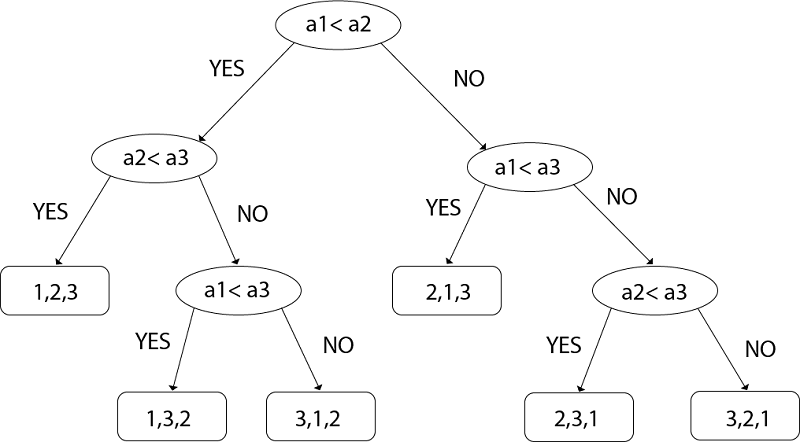
Daa Lower Bound Theory Javatpoint
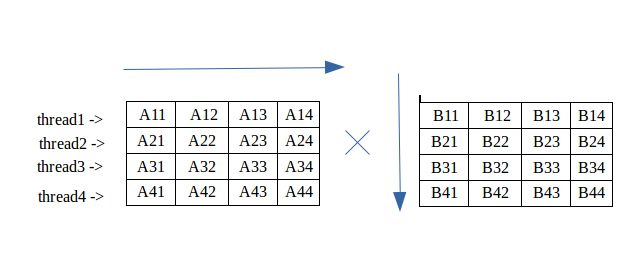
Multiplication Of Matrix Using Threads Geeksforgeeks

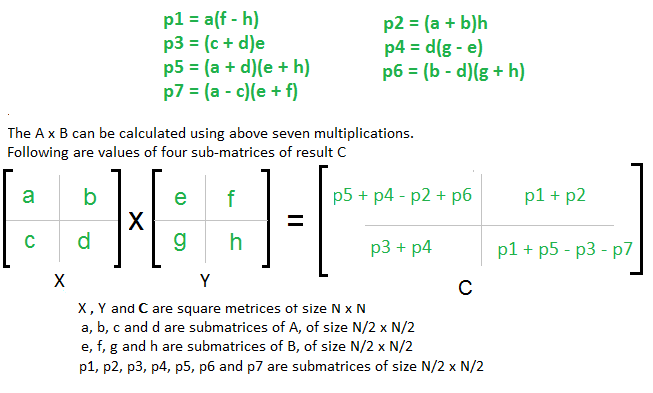
Easy Way To Remember Strassen S Matrix Equation Geeksforgeeks

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov