Matrix Product Wolfram Mathematica
1 2 2 3. Assuming matrix product refers to a computation Use as.
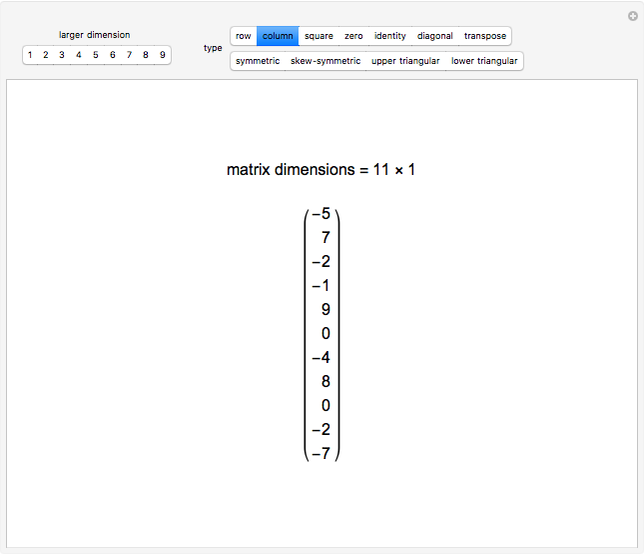
Some Special Types Of Matrices Wolfram Demonstrations Project
For example a nxm matrix can multiply a m-wide row vector without objection.

Matrix product wolfram mathematica. Flatten x. They can be entered directly with the notation constructed from a formula or imported from a data file. Cross v 1 v 2 gives the dual Hodge star of the wedge product.
Operator is specifically for tensor including vector and matrix multiplication. Based on the Wolfram Language Mathematica is 100 compatible with other core Wolfram products. If possible Mathematica also conforms the vectors as needed.
Knowledge-based broadly deployed natural language. Wolfram Natural Language Understanding System. This allows you to use a higher-level language to formulate the problem.
More deeply nested lists are by default printed with successive dimensions alternating between rows and columns. 2X3 can be multiplied to 3Xn through matrix multiplication or tensor product. W P w3 P.
They can act on any valid Mathematica expression they allow the use of any symbols to denote differential forms input - output notation is as close as possible to standard usage There are two. Stay on top of important topics and build connections by joining Wolfram Community groups relevant to your interests. Elements in each column are by default centered.
Mathematica Stack Exchange is a question and answer site for users of Wolfram Mathematica. In Mathematica the dot operator is overloaded and can be matrix multiplication matrix-vector multiplicationvector-matrix multiplication or the scalar dot product of vectors depending on context. B m c for matrix by using the flattening vectorizing relation Flatten a.
Solve the general linear matrix equation a 1. It defines the two basic operations - Exterior Product Wedge and Exterior Derivative d - in such a way that. The Wolfram Language also has commands for creating diagonal matrices constant matrices and other special matrix types.
For math science nutrition history. The Wolfram Language uses state-of-the-art algorithms to work with both dense and sparse matrices and incorporates a number of powerful original algorithms especially for high-precision and symbolic matrices. Wolfram Community forum discussion about Multiply two matrices.
The Wolfram Languages matrix operations handle both numeric and symbolic matrices automatically accessing large numbers of highly efficient algorithms. Mathematica is Wolframs original flagship productprimarily aimed at technical computing for RD and education. It is also possible to work with symbolic dimension specifications.
Version 12 provides new functionality for expressing vector matrix and tensor variables and conditions. Technology-enabling science of the computational universe. It only takes a minute to sign up.
The product of a normal matrix with a structured vector may have the structure of the vector. Matrix-Matrix Multiplication 9 Multiply real machine-number matrices. I am not sure how you want a 2X3 multiplied to a 3X3 matrix.
Valid dimension specifications d i in Matrices d 1 d 2 dom sym are positive integers. Matrix product - WolframAlpha. Cross x y gives the perpendicular vector - y x.
Valid component domain specifications dom are either Reals or Complexes. B a b. Solve Vector and Matrix Inequalities.
This example shows how such conditions can be used in equation and inequality solvers. Matrices d 1 d 2 uses Complexes by default. Compute answers using Wolframs breakthrough technology knowledgebase relied on by millions of students professionals.
This package enables Mathematica to carry out calculations with differential forms. Matrices are represented in the Wolfram Language with lists. I cant explain your statement that the product as you have it yields a scalar.
MatrixForm prints a single level list in a column. Referring to a mathematical definition. Just multiply without the.
I will utilize the Tensor Product first. S is a differentiation matrix approximating the second derivative in 1 dimension. B 1 a m.
It prints a two level list in standard matrix form. For matrices the symmetry sym can be either. In general Cross v 1 v 2 v n - 1 is a totally antisymmetric product which takes vectors of length n and yields a vector of length n that is orthogonal to all of the v i.
P 1 2 2 3. Since Mathematica hasnt defined what Dot a b means when a is a scalar and b is a matrix.

Multiplying A Matrix By A Number Wolfram Demonstrations Project

How To Get The Result Of A Multiplication Between A Matrix And A Vector Online Technical Discussion Groups Wolfram Community

Matrix Multiplication Wolfram Demonstrations Project

Matrix Inverse Calculator Wolfram Alpha
Wolfram Products Uni Software Plus
How Mathematica Made Wolfram Alpha Possible
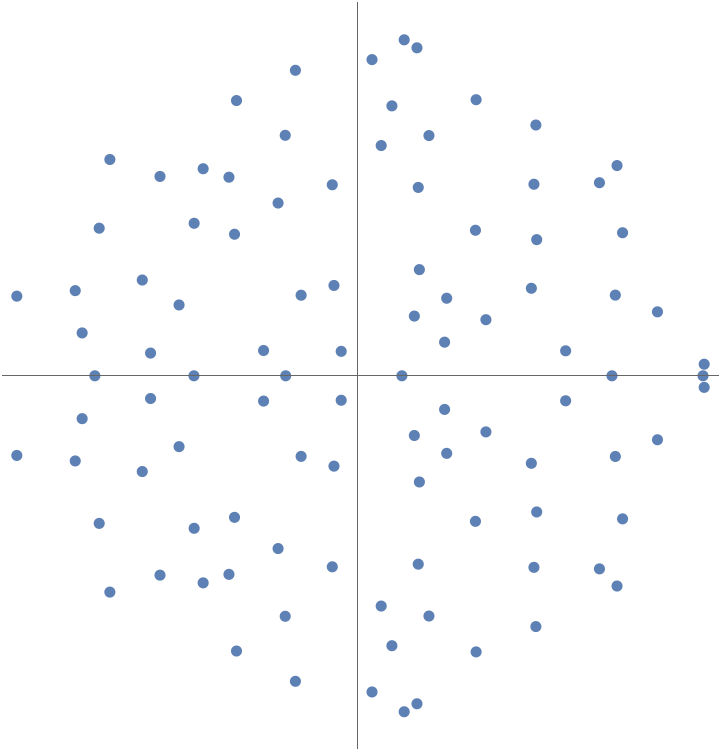
Eigenvalues Of A Random Matrix New In Wolfram Language 12
Multiply More Than 2 Matrices Online Technical Discussion Groups Wolfram Community

Mathematica Matrix Operations Youtube
Elementary Row Operations In Wolfram Alpha Online Technical Discussion Groups Wolfram Community

Matrix Multiplication Using Wolfram Alpha Youtube

Matrix Multiplication Wolfram Demonstrations Project

Determinant Calculator Wolfram Alpha

Basic Matrix Operations In Mathematica 10 Youtube

Solving Equations With Wolfram Alpha Wolfram Alpha Blog
How To Test For Row Equivalence Of Two Matrices Using Wolfram Alpha Online Technical Discussion Groups Wolfram Community
Notebook Documents Mathematica Wolfram Language For Math Students Fast Intro

