Dot Product Of Two Matrices Matlab
You can write this definition using the MATLAB colon operator as. However A and B are not the same size so dot AB function can not be performed successfullly.
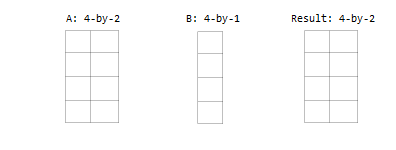
Compatible Array Sizes For Basic Operations Matlab Simulink
The Dot Product block generates the dot product of the input vectors.
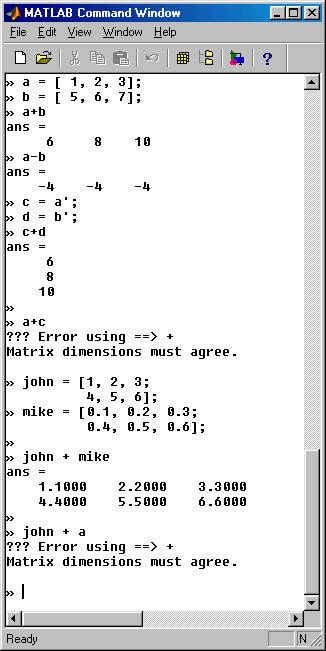
Dot product of two matrices matlab. To perform dot product function it is mathematical need that you have 2 matrices where dimensions of matrices agree. Here we discuss an introduction to Dot Product MATLAB syntax examples with sample code. The result is a 1-by-1 scalar also called the dot product or inner product of the vectors A and B.
The scalar output y is equal to the MATLAB operation y sum conj u1 u2 where u1 and u2 represent the input vectors. The dot product inner product of two vectors has the following properties. The dot product also called scalar product of the vectors a and b is written as a b and defined to be a b abcosφ where a and b is the magnitudes of the two vectors and φ is the angle between the two vectors.
So i converted them to Matrix of dimension 6138x3. Multiply B times A. Alternatively you can calculate the dot product with the syntax dot AB.
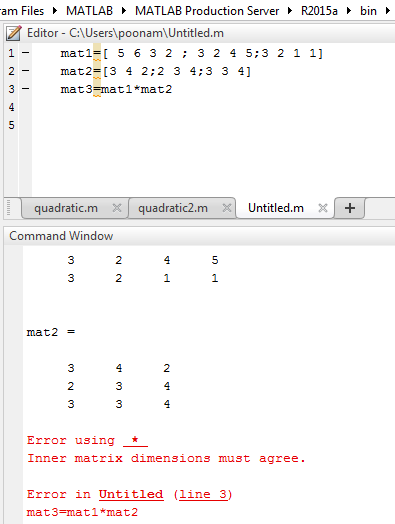
You can also go through. C AB is the matrix product of A and B. You cannot make a dot product function that would multiply two matrices where dimensions dont agree.
When two vectors are in unit-vector notation their dot product is written as. Dot function is used in MATLAB to find the dot product of vectors or scalars in MATLAB. Now when I used dot PZ I am getting a 1x3 matrix.
Dot product between two different size of matrix. X y u v cosθ where θ is the angle between the vectors. When x and y are orthogonal their dot product is zero.
I have two vectors P and Z and they both have 6138 data points. And I would like to calculate the dot product of dot AB. I have two matrix one is A 1by 3 matrix the other one is B 86 by 3 matrix.
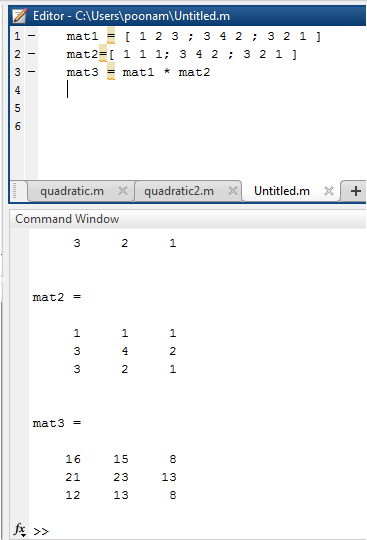
This is a guide to Dot Product MATLAB. A b a1i a2j a3kb1i b2j b3k and the result is a b a1b1 a2b2 a3b3. For finding the dot product of matrices the columns in the 1st matrix must be equal in number to rows in the 2nd matrix.
C 44 1 1 0 0 2 2 0 0 3 3 0 0 4 4 0 0. As we all know the dot product of 2 vectors must be a scalar quantity. B a b cos theta We will use this formula later to find the angle theta.
When the dot function in Matlab is called on two 2D matrices the dot product is computed for each set of columns. Thus for each column you get a scalar result which is why the answer is returned as 1x11. The dot product of two vectors multiplies each element together then sums the result to produce one number.
If A is an m-by-p and B is a p-by-n matrix then C is an m-by-n matrix defined by This definition says that C ij is the inner product of the i th row of A with the j th column of B. There needs to be the same amount of rows of first matrix as the number of columns of second matrix. The dot product or scalar product of two vectors is used among other things as a way of finding the angle theta between two vectors.
Recall that given vectors a and b in space the dot product is defined as.
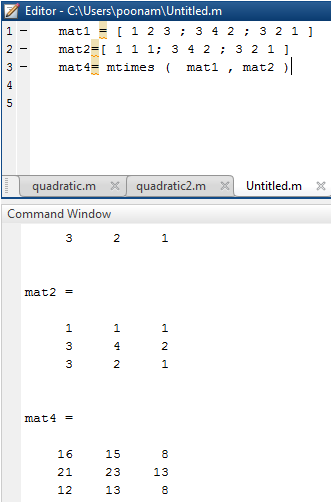
Matrix Multiplication In Matlab How To Perform Matrix Multiplication
Matlab Tutorial 25 Calculating The Vector Dot Product And Cross Product Youtube
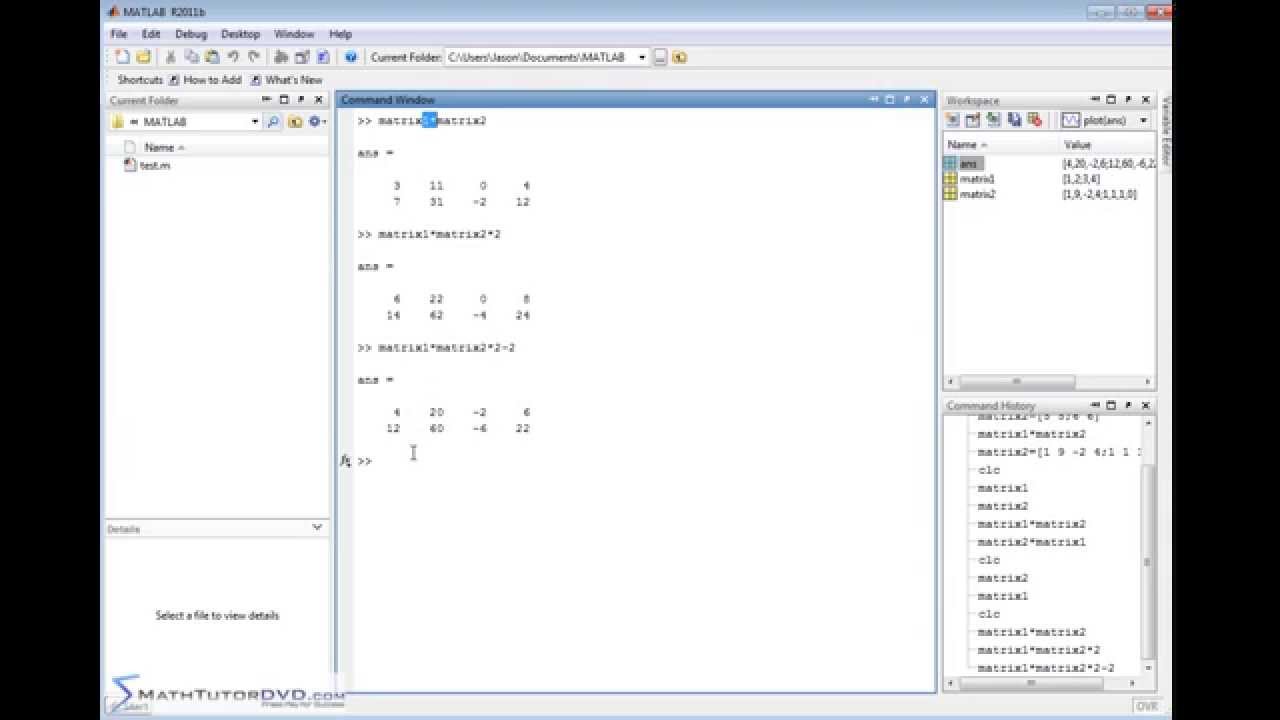
Matlab Tutorial Multiplying Matrices Youtube
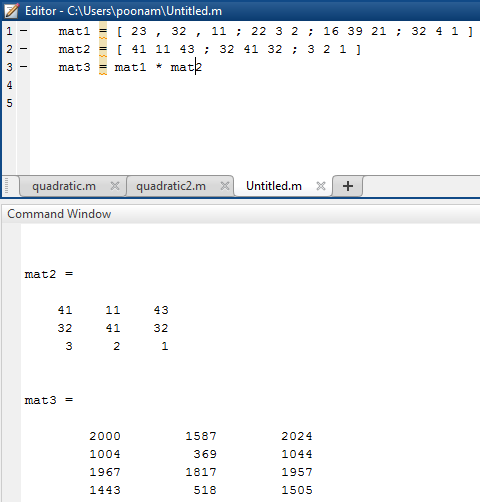
Matrix Multiplication In Matlab How To Perform Matrix Multiplication
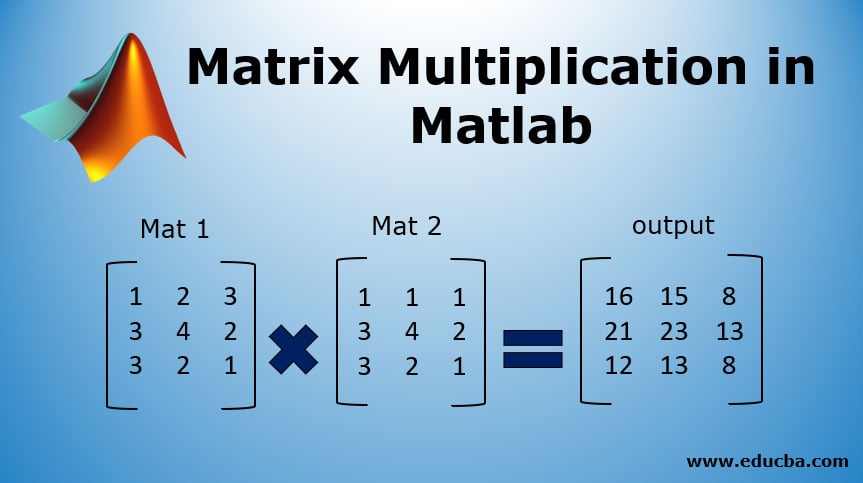
Matrix Multiplication In Matlab How To Perform Matrix Multiplication
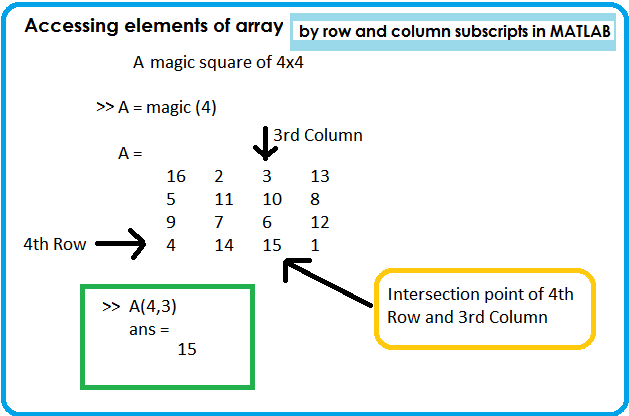
Matrices And Arrays In Matlab Javatpoint
Matrix Multiplication In Matlab How To Perform Matrix Multiplication

Matlab Entering Constructing Displaying Arrays

How To Make A Matrix In A Loop In Matlab Video Matlab

Matlab Video Tutorial Multiplying Matrices And Vectors Youtube

Matlab Cross Product Learn How To Implement Cross Product In Matlab

Matrix In Matlab Creating And Manipulating Matrices In Matlab
Matrix Multiplication In Matlab How To Perform Matrix Multiplication

Matlab Entering Constructing Displaying Arrays

Making A Matrix In A Loop In Matlab Stuart S Matlab Videos Matlab Simulink



